题目内容
【题目】已知函数![]()
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)证明:若![]() 存在零点,则
存在零点,则![]() 在区间
在区间![]() 上仅有一个零点.
上仅有一个零点.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)见解析
(Ⅲ)见解析
【解析】
(Ⅰ)求得![]() 时
时![]() 的导数,可得切线的斜率和切点,可得切线方程;(Ⅱ)若
的导数,可得切线的斜率和切点,可得切线方程;(Ⅱ)若![]() 对
对![]() 恒成立,即为
恒成立,即为![]() 对
对![]() 恒成立,设
恒成立,设![]() ,求得导数和单调性、极大值即最大值,可得
,求得导数和单调性、极大值即最大值,可得![]() 的范围;(Ⅲ)若
的范围;(Ⅲ)若![]() 存在零点,即关于
存在零点,即关于![]() 的方程
的方程![]() 有解,可得
有解,可得![]() 有解,由
有解,由![]() 的单调性,即可得证.
的单调性,即可得证.
(Ⅰ)当![]() 时,
时,![]() ,
,![]()
所以![]() ,
,![]()
所以切线方程为![]()
(Ⅱ)![]() 对
对![]() 恒成立
恒成立
等价于![]() ,即
,即![]() 恒成立
恒成立
设![]() ,则
,则![]()
由![]() 解得
解得![]()
![]() 与
与![]() 在区间
在区间![]() 上的情况如下
上的情况如下
|
|
|
|
|
| 0 |
|
| 增 | 极大 | 减 |
所以函数![]() 的单调增区间是
的单调增区间是![]() ,单调减区间是
,单调减区间是![]() .
.
函数![]() 在
在![]() 处取得极大值(也是最大值)
处取得极大值(也是最大值)![]()
所以![]() ,即
,即![]() 的取值范围是
的取值范围是![]()
(Ⅲ)若函数![]() 存在零点,则关于
存在零点,则关于![]() 的方程
的方程![]() 有解,
有解,
即方程![]() 有解,
有解,
由(Ⅱ)可知函数![]() 的单调增区间是
的单调增区间是![]() ,单调减区间是
,单调减区间是![]() ,
,
因为![]() ,所以当
,所以当![]() 时,
时,![]() ,
,
又因为当![]() 时,
时,![]() ,
,
所以若方程![]() 有解,则在
有解,则在![]() 上仅有一个解,
上仅有一个解,
即若![]() 存在零点,则
存在零点,则![]() 在
在![]() 上仅有一个零点.
上仅有一个零点.

【题目】以下是某地区不同身高的未成年男性的体重平均值表.
身高/ | 60 | 70 | 80 | 90 | 100 | 110 |
体重/ | 6.13 | 7.9 | 9.99 | 12.15 | 15.02 | 17.5 |
身高/ | 120 | 130 | 140 | 150 | 160 | 170 |
体重/ | 20.92 | 26.86 | 31.11 | 38.85 | 42.25 | 55.05 |
(1)给出两个回归方程:
①![]() ,②
,②![]() .通过计算,得到它们的相关指数分别是:
.通过计算,得到它们的相关指数分别是:![]() ,
,![]() .试问哪个回归方程拟合效果更好?
.试问哪个回归方程拟合效果更好?
(2)若体重超过相同身高男性平均值的1.2倍为偏胖,低于0.8为偏瘦,那么该地区某中学一男生身高为![]() ,体重为
,体重为![]() ,他的体重是否正常?
,他的体重是否正常?
【题目】已知某校5个学生的数学和物理成绩如下:
学生的编号 | 1 | 2 | 3 | 4 | 5 |
数学成绩 | 80 | 75 | 70 | 65 | 60 |
物理成绩 | 70 | 66 | 68 | 64 | 62 |
(1)通过大量事实证明发现,一个学生的数学成绩和物理成绩是具有很强的线性相关关系的,在上述表格中,用![]() 表示数学成绩,用
表示数学成绩,用![]() 表示物理成绩,求
表示物理成绩,求![]() 关于
关于![]() 的回归方程.
的回归方程.
(2)利用残差分析回归方程的拟合效果,若残差和在![]() 范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
(3)现从5名同学中任选两人参加访谈活动,求1号同学没被选中的概率.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: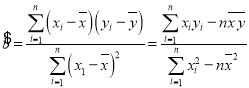 ,
,![]() .
.

