题目内容
已知点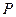 为圆周
为圆周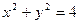 的动点,过
的动点,过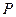 点作
点作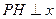 轴,垂足为
轴,垂足为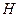 ,设线段
,设线段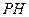 的中点为
的中点为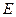 ,记点
,记点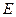 的轨迹方程为
的轨迹方程为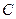 ,点
,点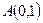
(1)求动点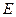 的轨迹方程
的轨迹方程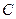 ;
;
(2)若斜率为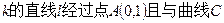 的另一个交点为
的另一个交点为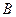 ,求
,求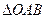 面积的最大值及此时直线
面积的最大值及此时直线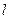 的方程;
的方程;
(3)是否存在方向向量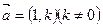 的直线
的直线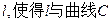 交与两个不同的点
交与两个不同的点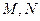 ,且有
,且有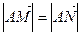 ?若存在,求出
?若存在,求出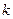 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
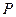 为圆周
为圆周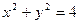 的动点,过
的动点,过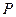 点作
点作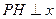 轴,垂足为
轴,垂足为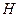 ,设线段
,设线段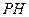 的中点为
的中点为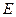 ,记点
,记点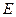 的轨迹方程为
的轨迹方程为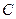 ,点
,点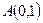
(1)求动点
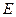 的轨迹方程
的轨迹方程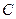 ;
;(2)若斜率为
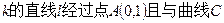 的另一个交点为
的另一个交点为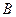 ,求
,求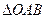 面积的最大值及此时直线
面积的最大值及此时直线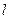 的方程;
的方程;(3)是否存在方向向量
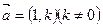 的直线
的直线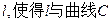 交与两个不同的点
交与两个不同的点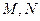 ,且有
,且有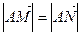 ?若存在,求出
?若存在,求出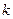 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。(1)设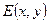 ,则
,则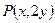 ,而
,而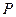 点在圆上
点在圆上
所以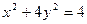 ,即
,即
(2)
而 ,故当
,故当 时,
时,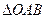 面积的最大值为1
面积的最大值为1
此时,直线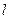 的方程为:
的方程为: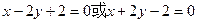
(3)假设存在符合题设条件的直线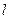 ,设其方程为:
,设其方程为: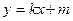
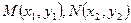 ,
,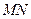 的中点
的中点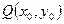
于是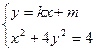
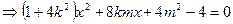

 ………………………………………1
………………………………………1
而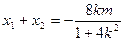
故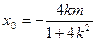 从而
从而
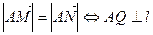 而
而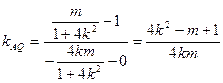
故
可得: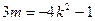 ……………………………………2
……………………………………2
由1和2得: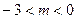
故
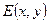 ,则
,则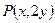 ,而
,而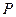 点在圆上
点在圆上所以
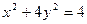 ,即
,即
(2)

而
 ,故当
,故当 时,
时,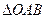 面积的最大值为1
面积的最大值为1此时,直线
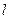 的方程为:
的方程为: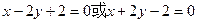
(3)假设存在符合题设条件的直线
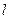 ,设其方程为:
,设其方程为: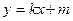
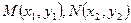 ,
,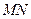 的中点
的中点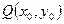
于是
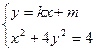
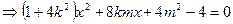

 ………………………………………1
………………………………………1而
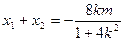
故
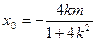 从而
从而
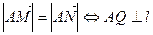 而
而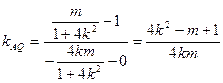
故

可得:
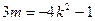 ……………………………………2
……………………………………2由1和2得:
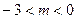
故

略

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
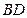 是△
是△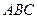 的角平分线,∠
的角平分线,∠
 ,
,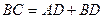 ,求证
,求证
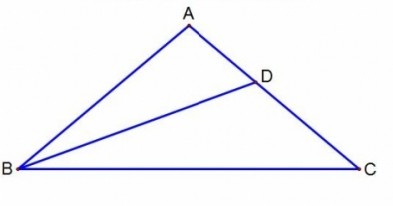
 的实轴长是( )
的实轴长是( )

 上一点M到左焦点
上一点M到左焦点 的距离为2,N是
的距离为2,N是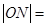 ( )
( )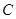 :
: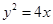 的准线与对称轴相交于点
的准线与对称轴相交于点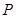 ,过点
,过点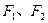 为椭圆
为椭圆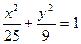 的两个焦点,过
的两个焦点,过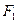 的直线交椭圆于
的直线交椭圆于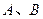 两点,若
两点,若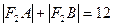 ,则
,则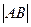 =
=  ,
, ),且与直线l:y=
),且与直线l:y= 相切
相切 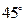 ,求Q点横坐标.
,求Q点横坐标.