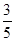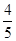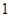题目内容
在△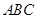 中,角
中,角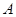 ,
,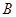 ,
,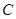 所对的边分别为
所对的边分别为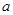 ,
,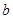 ,
,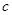 .
.
(1)若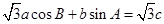 ,求角
,求角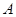 ;
;
(2)若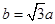 ,
,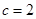 ,且△
,且△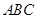 的面积为
的面积为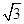 ,求
,求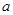 的值.
的值.
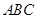 中,角
中,角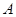 ,
,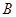 ,
,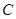 所对的边分别为
所对的边分别为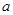 ,
,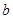 ,
,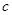 .
.(1)若
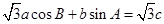 ,求角
,求角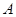 ;
;(2)若
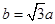 ,
,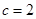 ,且△
,且△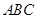 的面积为
的面积为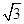 ,求
,求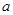 的值.
的值.(1) (2)
(2)
 (2)
(2)
试题分析:(1)将已知
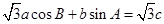 应用正弦定理转化为纯角的关系,并用
应用正弦定理转化为纯角的关系,并用 将角C用角A,B表示,再注意到
将角C用角A,B表示,再注意到 ,从而可求得角A的三角函数值,从而得到角A的大小;(2)由于
,从而可求得角A的三角函数值,从而得到角A的大小;(2)由于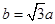 和△
和△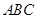 的面积为
的面积为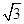
 ,可将
,可将 用含量a的代数式表示出来,再由
用含量a的代数式表示出来,再由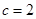 应用余弦定理就可将
应用余弦定理就可将 用含a的代数式表示,最后注意到
用含a的代数式表示,最后注意到 ,从而就可得到关于a的一个一元方程,解此方程就可得到a的值.
,从而就可得到关于a的一个一元方程,解此方程就可得到a的值.试题解析:(1)
 ,由正弦定理可得
,由正弦定理可得
 .
.即
 .
.即


 ,
, .
.注:利用
 直接得
直接得 同样给分
同样给分(2)

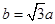 ,
, 的面积为
的面积为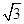 ,
,
 .
. ,
, ①
①由余弦定理


 ,
, ②
②由①,②得:
 , 化简得
, 化简得 ,
,  ,
,

(2)或解:由
 得
得  ①
①由
 得
得  ②
②由①,②得:
 ,即
,即 ,
,  ,
, .
.
 .
.
练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
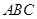 中,已知
中,已知 ,向量
,向量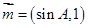 ,
,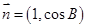 ,且
,且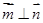 .
.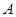 的值;
的值;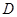 在边
在边 上,且
上,且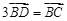 ,
,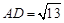 ,求△
,求△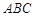 的面积.
的面积. ,
, ,
, 是的内角,
是的内角, ,
, ,
, 分别是其对边长,向量,,.
分别是其对边长,向量,,. +2,且sinA+sinB=
+2,且sinA+sinB= sinC,求角C的度数.
sinC,求角C的度数.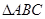 中,角
中,角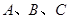 所对的边分别为
所对的边分别为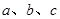 ,那么下列给出的各组条件能确定三角形有两解的是( )
,那么下列给出的各组条件能确定三角形有两解的是( )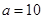 ,
,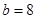 ,
,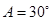
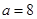 ,
,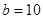 ,
,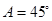
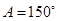
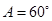
 中,
中, ,
,
 的值;
的值; 的长
的长
 中,设角
中,设角 所对边分别为
所对边分别为 ,若
,若 ,则角
,则角 .
. 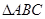 中,若
中,若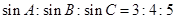 ,则
,则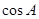 的值为
的值为