题目内容
△ABC中,a、b、c分别是角A、B、C的对边,△ABC的周长为 +2,且sinA+sinB=
+2,且sinA+sinB= sinC.(1)求边c的长. (2)若△ABC的面积为
sinC.(1)求边c的长. (2)若△ABC的面积为 sinC,求角C的度数.
sinC,求角C的度数.
 +2,且sinA+sinB=
+2,且sinA+sinB= sinC.(1)求边c的长. (2)若△ABC的面积为
sinC.(1)求边c的长. (2)若△ABC的面积为 sinC,求角C的度数.
sinC,求角C的度数.(1)c= ;(2) ∠C=60°.
;(2) ∠C=60°.
 ;(2) ∠C=60°.
;(2) ∠C=60°.试题分析:(1)由正弦定理可知: sinA+sinB=
 sinC等价于a+b=
sinC等价于a+b= c代入已知a+b+c=
c代入已知a+b+c= +2可求得边c的长; (2)由三角形的面积公式可得S△ABC=
+2可求得边c的长; (2)由三角形的面积公式可得S△ABC=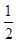 absinC=
absinC= sinC,又注意到sinC>0得ab=
sinC,又注意到sinC>0得ab=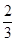 ,结合(1)中结论,并注意到a+b=2,应用余弦定理cosC=
,结合(1)中结论,并注意到a+b=2,应用余弦定理cosC=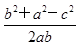 =
=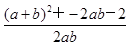 可求得cosC值,进而得到角C的度数.
可求得cosC值,进而得到角C的度数.试题解析:(1)在△ABC中,∵sinA+sinB=
 sinC,
sinC,由正弦定理,得a+b=
 c, 3分
c, 3分∴a+b+c=
 c+c=(
c+c=( +1)c=
+1)c= +2.
+2.∴a+b=2,c=
 6分。
6分。(2)在△ABC中,S△ABC=
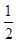 absinC=
absinC= sinC,
sinC,∴
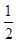 ab=
ab= ,即ab=
,即ab=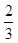 8分
8分又a+b=2,在△ABC中,由余弦定理,
得cosC=
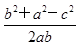 =
=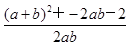 =
=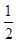 , .10分
, .10分又在△ABC中∠C∈(0,π),
∴∠C=60° .12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
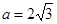 ,
,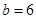 ,
,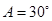 ,求B及S
,求B及S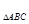 .
.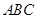 中,角
中,角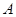 ,
,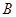 ,
,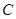 所对的边分别为
所对的边分别为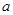 ,
,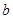 ,
,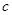 .
.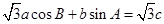 ,求角
,求角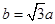 ,
,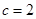 ,且△
,且△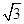 ,求
,求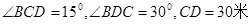 ,并在点C测得塔顶A的仰角为
,并在点C测得塔顶A的仰角为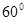 ,求塔高AB.
,求塔高AB.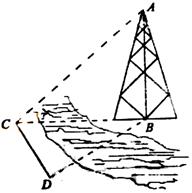
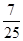
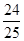
 ,求角A;(2)若
,求角A;(2)若 ,求△ABC的面积.
,求△ABC的面积.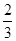 ,sinB=
,sinB=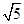 cosC.
cosC.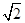 ,求△ABC的面积.
,求△ABC的面积.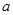 ,
,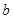 ,
,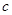 .若
.若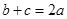 ,
,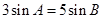 ,则角
,则角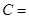 ( )
( )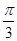
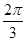
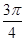
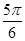
 中,内角
中,内角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
, ,则
,则 等于( )
等于( )
