题目内容
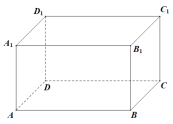
【题目】如图所示的长方体![]() ,
,![]() . 动点
. 动点![]() 在该长方体外接球上,且
在该长方体外接球上,且![]() ,则点
,则点![]() 的轨迹长度为( )
的轨迹长度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
求出长方体外接球的半径,在平面ABCD上确定满足条件的一点![]() ,根据题意可得
,根据题意可得![]() 点的轨迹是过弦
点的轨迹是过弦![]() 且垂直于平面ABCD的平面与长方体外接球所截得的圆,作出图形,数形结合求出此圆的周长即为轨迹长度.
且垂直于平面ABCD的平面与长方体外接球所截得的圆,作出图形,数形结合求出此圆的周长即为轨迹长度.
由题意知长方体外接球的半径为![]() ,
,
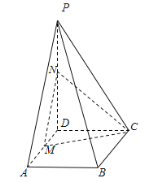
因为![]() 是长方体外接球表面上一点,且
是长方体外接球表面上一点,且![]() ,如图,
,如图,

点![]() 是其中满足条件的一点,且
是其中满足条件的一点,且![]() ,
,![]()
可知![]() 点的轨迹是过弦
点的轨迹是过弦![]() 且垂直于平面
且垂直于平面![]() 的平面与长方体外接球所截得的圆,
的平面与长方体外接球所截得的圆,
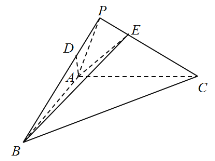
设该圆圆心为![]() ,外接球球心为O,平面ABCD所在圆圆心为
,外接球球心为O,平面ABCD所在圆圆心为![]() ,
,
如图,只需求圆![]() 的周长,设半径
的周长,设半径![]() ,
,

∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ∴
∴![]() ,又
,又![]() ,
,
∴![]() ,在
,在![]() 中,
中,![]() 是中位线,则
是中位线,则![]() ,
,
而![]() ,∴
,∴![]() ,
,
∴![]() 点的轨迹长度是
点的轨迹长度是![]() .
.
故选D.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目