题目内容
如图,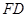 垂直于矩形
垂直于矩形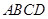 所在平面,
所在平面,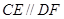 ,
, .
.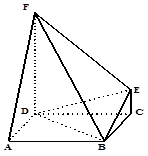
(1)求证: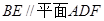 ;
;
(2)若矩形 的一个边
的一个边 ,
, ,则另一边
,则另一边 的长为何值时,三棱锥
的长为何值时,三棱锥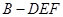 的体积为
的体积为 ?
?
(1)证明详见解析;(2)当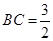 时,三棱锥
时,三棱锥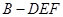 的体积为
的体积为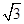 .
.
解析试题分析:(1)要证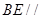 面
面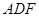 ,只须在平面
,只须在平面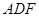 内找一条直线与
内找一条直线与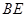 平行,过点
平行,过点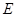 作
作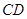 的平行线交
的平行线交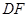 于点
于点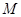 ,连接
,连接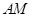 ,
,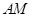 就是所要找的直线,这时只须充分利用题中的平行条件即可证明
就是所要找的直线,这时只须充分利用题中的平行条件即可证明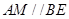 ,从而问题得证;(2)由(1)的证明过程得到
,从而问题得证;(2)由(1)的证明过程得到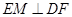 且
且 ,在
,在 中,先利用
中,先利用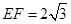 、
、 确定
确定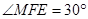 ,进一步算出
,进一步算出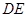 ,从而就确定了三棱锥
,从而就确定了三棱锥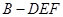 的底面积
的底面积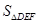 ,由题中的垂直条件易得
,由题中的垂直条件易得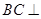 平面
平面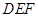 ,再由所给的体积及三棱锥的体积计算公式可求出
,再由所给的体积及三棱锥的体积计算公式可求出 的长度,问题得以解决.
的长度,问题得以解决.
试题解析:(1)过点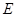 作
作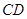 的平行线交
的平行线交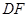 于点
于点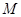 ,连接
,连接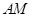 ,则
,则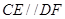
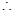 四边形
四边形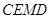 是平行四边形
是平行四边形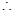
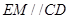 且
且 ,又
,又 且
且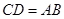
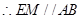 且
且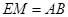
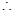 四边形
四边形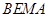 也是平行四边形
也是平行四边形 ,
,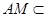 平面
平面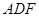 ,
,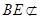 面
面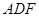
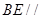 面
面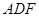 6分
6分
(2)由(1)可知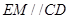 且
且 面
面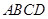
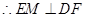
在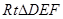 中,
中,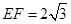 ,
, ,得
,得 且
且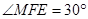
由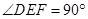 可得
可得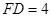 ,从而得
,从而得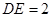
因为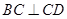 ,
,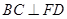 ,所以
,所以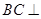 平面
平面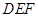
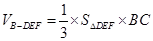 ,而
,而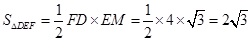 且
且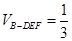
所以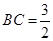
综上,当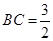 时,三棱锥
时,三棱锥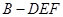 的体积为
的体积为 12分.
12分.
考点:1.空间中的平行关系;2.三棱锥的体积计算公式.

练习册系列答案
相关题目
 ,
, ,
, ,
, .又
.又 ,
, ,
, ,直线
,直线 与直线
与直线 所成的角为60°.
所成的角为60°. ;
; 的体积.
的体积.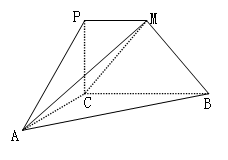
 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形, 为
为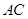 与
与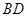 的交点,
的交点,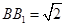 ,
,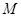 是线段
是线段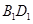 的中点.
的中点.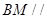 平面
平面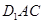 ;
;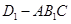 的体积.
的体积.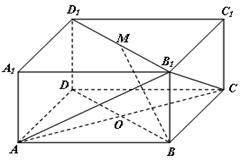
 中,
中,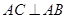 ,
, 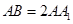 ,
,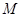 是
是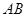 的中点,△
的中点,△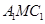 是等腰三角形,
是等腰三角形,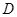 为
为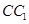 的中点,
的中点,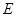 为
为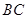 上一点.
上一点.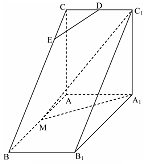
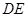 ∥平面
∥平面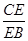 ;
;
 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.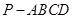 中,底面
中,底面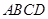 为直角梯形,且
为直角梯形,且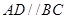 ,
,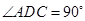 ,平面
,平面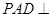 底面
底面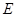 为
为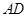 的中点,
的中点, 是棱
是棱 的中点,
的中点,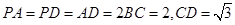 .
.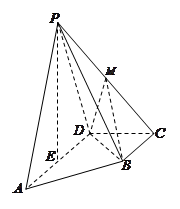
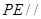 平面
平面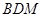 ;
;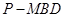 的体积.
的体积.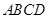 中,
中,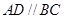 ,
,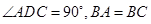 .把
.把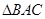 沿
沿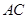 折起到
折起到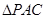 的位置,使得
的位置,使得 点在平面
点在平面 上的正投影
上的正投影 恰好落在线段
恰好落在线段 分别为棱
分别为棱 的中点.
的中点.
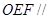 平面
平面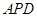 ;
;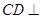 平面
平面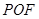 ;
; ,求四棱锥
,求四棱锥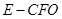 的体积.
的体积.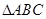 是边长为6的等边三角形,
是边长为6的等边三角形,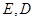 分别为
分别为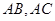 靠近
靠近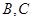 的三等分点,点
的三等分点,点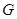 为边
为边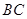 边的中点,线段
边的中点,线段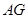 交线段
交线段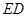 于点
于点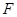 .将
.将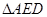 沿
沿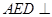 平面
平面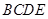 ,连接
,连接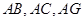 ,形成如图乙所示的几何体.
,形成如图乙所示的几何体.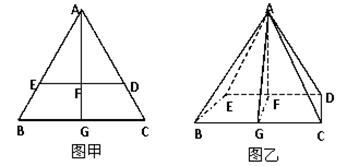
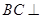 平面
平面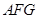
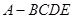 的体积.
的体积. 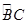 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图(2)所示).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图(2)所示).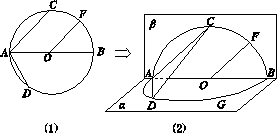
 上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求点G到平面ACD的距离;若不存在,请说明理由.
上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求点G到平面ACD的距离;若不存在,请说明理由.