题目内容

18．已知数列{1+an}是以2为公比的等比数列，且a1=1，则a5=（　　）
A．31B．24C．21D．7

分析 先利用数列{1+an}是以2为公比的等比数列以及a1=1，求出数列{1+an}的通项，再把n=5代入即可求出结论．

解答 解：因为数列{1+an}是以2为公比的等比数列，且a1=1，
所以其首项为1+a1=2．
其通项为：1+an=（1+a1）×2n-1=2n．
当n=4时，1+a5=25=32．
所以a5=31．
故选：A．

点评 本题主要考查等比数列的性质的应用．解决本题的关键在于利用数列{1+an}是以2为公比的等比数列以及a1=1，求出数列{1+an}的通项．是对基础知识的考查，属于基础题．

练习册系列答案
相关题目
20．在明朝程大位所著《算法统宗》中，有这样的一首歌谣，叫做浮屠增级歌．“远看巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”这首古诗描述的这个宝塔其古称浮屠，它一共有七层，每层悬挂的红灯数是上一层的2倍，全塔总共有381盏灯，问塔顶有几盏灯？据此，你算出顶层悬挂的红灯的盏数为（　　）
A．5B．4C．3D．4
9．在△ABC中，若sin2A-sinAsinB-sin2C+sin2B=0，且acosB=bcosA，则三角形的形状是等边三角形．
6．已知函数$f（x）=lnx+\frac{1}{x}$．
（1）求f（x）的最小值；
（2）若方程f（x）=a有两个根x1，x2（x1＜x2），证明：x1+x2＞2．
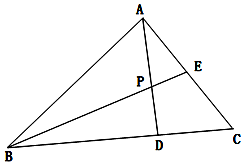13．在△ABC中，E为AC中点，D为BC靠近C的三等分点，记$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AC}$=$\overrightarrow b$．
（1）用$\overrightarrow a，\overrightarrow b$表示$\overrightarrow{AD}，\overrightarrow{BE}$；
（2）求BP：PE，并用$\overrightarrow a，\overrightarrow b$表示$\overrightarrow{CP}$．
3．化简cos96°cos24°-sin96°sin24°=-$\frac{1}{2}$．
10．已知 A={y|y＞1}，B={x|lnx≥0}，则A∩B=（　　）
A．{x|x≥1}B．{x|x＞1}C．{x|0＜x＜1}D．∅
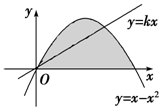7．如图直线y=kx及抛物线y=x-x2
（1）当k=$\frac{1}{2}$时，求由直线y=kx及抛物线y=x-x2围成的平面图形的面积；
（2）若直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分，求k的值．
8．若$C_n^{10}=C_n^8$，则$C_{20}^n$=（　　）
A．380B．190C．18D．9

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网