题目内容
10.已知定义在R上的奇函数f(x)的导函数为f′(x),当x<0时,f(x)满足2f(x)+xf′(x)<xf(x),则f(x)在R上的零点的个数为0.分析 构造函数F(x)=$\frac{{x}^{2}f(x)}{{e}^{x}}$ (x<0),求函数的导数,利用导数判断其单调性,结合函数为奇函数,即可得出结论.
解答 解:构造函数F(x)=$\frac{{x}^{2}f(x)}{{e}^{x}}$ (x<0),
则F′(x)=$\frac{2xf(x){e}^{x}+{x}^{2}f′(x){e}^{x}-{x}^{2}f(x){e}^{x}}{{(e}^{x})^{2}}$=$\frac{x[2f(x)+xf′(x)-xf(x)]}{{e}^{x}}$,
∵当x<0时,f(x)满足2f(x)+xf′(x)<xf(x),
∴F′(x)>0,
即函数F(x)在x<0时是增函数,
又F(0)=0,
∴当x<0,F(x)<F(0)=0成立,
∵对任意x<0,$\frac{{x}^{2}}{{e}^{x}}$>0,∴f(x)<0,
∵f(x)是奇函数,
∴x>0时,f(x)>0,
即f(x)=0只有一个根就是0.
故答案为:0
点评 本题考查了函数零点个数求解;根据条件构造函数F(x)=$\frac{{x}^{2}f(x)}{{e}^{x}}$是解决本题的关键.综合考查函数单调性和导数的关系.

练习册系列答案
相关题目
5.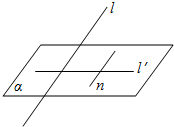 如图,设直线l是平面α的一条射线,l′是l在α内的射影,直线n?α.用<a,b>表示直线a,b的夹角.求证:
如图,设直线l是平面α的一条射线,l′是l在α内的射影,直线n?α.用<a,b>表示直线a,b的夹角.求证:
(1)cos<l,n>=cos<l,l′>•cos<l′,n>;
(2)n⊥l?n⊥l′.
 如图,设直线l是平面α的一条射线,l′是l在α内的射影,直线n?α.用<a,b>表示直线a,b的夹角.求证:
如图,设直线l是平面α的一条射线,l′是l在α内的射影,直线n?α.用<a,b>表示直线a,b的夹角.求证:(1)cos<l,n>=cos<l,l′>•cos<l′,n>;
(2)n⊥l?n⊥l′.
2.已知函数f(x)=ax3+bx2+cx+d的图象如图所示,则下列判断正确的是( )


| A. | a<0,b<0,c<0 | B. | a>0,b>0,c<0 | C. | a>0,b<0,c>0 | D. | a>0,b>0,c>0 |
20.已知a>0且a≠1,函数f(x)=loga(x2-ax+$\frac{1}{2}$)有最小值,则实数a的取值范围是( )
| A. | (0,1) | B. | (0,1)∪(1,$\sqrt{2}$) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,+∞) |
 中,角
中,角 的对边分别为
的对边分别为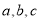 ,且三角形的面积为
,且三角形的面积为 .
. 的大小;
的大小; ,求
,求 的值.
的值.