题目内容
(本小题共13分)已知函数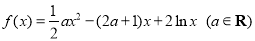 .
.
(Ⅰ)若曲线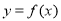 在
在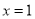 和
和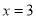 处的切线互相平行,求
处的切线互相平行,求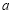 的值;
的值;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)设 ,若对任意
,若对任意 ,均存在
,均存在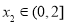 ,使得
,使得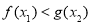 ,
,
求 的取值范围.
的取值范围.
(Ⅰ)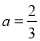 ;(Ⅱ)当
;(Ⅱ)当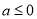 时,
时,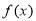 的单调递增区间是
的单调递增区间是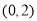 ,单调递减区间是
,单调递减区间是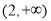 ;当
;当 时;
时;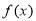 的单调递增区间是
的单调递增区间是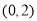 和
和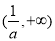 ,单调递减区间是
,单调递减区间是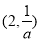 .;当
.;当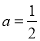 时,
时,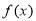 的单调递增区间是
的单调递增区间是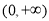 ;当
;当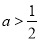 时,
时,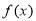 的单调递增区间是
的单调递增区间是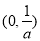 和
和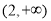 ,单调递减区间是
,单调递减区间是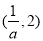 .;(Ⅲ)
.;(Ⅲ)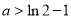
【解析】
试题分析: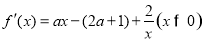 . 2分
. 2分
(Ⅰ)根据题意,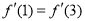 ,解得
,解得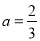 . 4分
. 4分
(Ⅱ)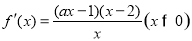 . 5分
. 5分
①当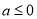 时,
时,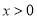 ,
,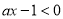 ,
,
在区间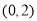 上,
上,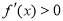 ;在区间
;在区间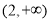 上
上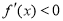 ,
,
故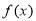 的单调递增区间是
的单调递增区间是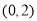 ,单调递减区间是
,单调递减区间是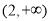 . 6分
. 6分
②当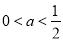 时,
时,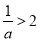 ,
,
在区间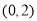 和
和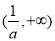 上,
上,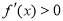 ;在区间
;在区间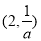 上
上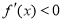 ,
,
故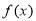 的单调递增区间是
的单调递增区间是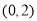 和
和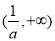 ,单调递减区间是
,单调递减区间是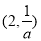 . 7分
. 7分
③当 时,
时,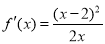 , 故
, 故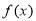 的单调递增区间是
的单调递增区间是 . 8分
. 8分
④当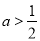 时,
时,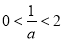 ,
,
在区间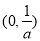 和
和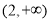 上,
上,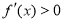 ;在区间
;在区间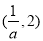 上
上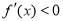 ,
,
故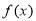 的单调递增区间是
的单调递增区间是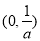 和
和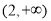 ,单调递减区间是
,单调递减区间是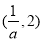 . 9分
. 9分
(Ⅲ)由已知,在 上有
上有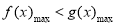 . 10分
. 10分
由已知,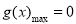 ,由(Ⅱ)可知,
,由(Ⅱ)可知,
①当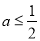 时,
时,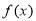 在
在 上单调递增,
上单调递增,
故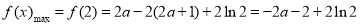 ,
,
所以,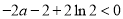 ,解得
,解得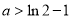 ,故
,故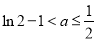 . 11分
. 11分
②当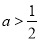 时,
时,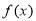 在
在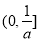 上单调递增,在
上单调递增,在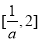 上单调递减,
上单调递减,
故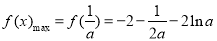 .
.
由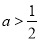 可知
可知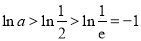 ,
,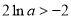 ,
,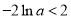 ,
,
所以,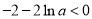 ,
,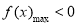 , 12分
, 12分
综上所述,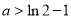 . 13分
. 13分
考点:本题考查利用导数研究曲线的切线,利用导数研究函数的单调性,以及最值

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
 满足
满足 ,则
,则 的最大值为 .
的最大值为 . ,若
,若 存在唯一的零点
存在唯一的零点 ,且
,且 ,则常数
,则常数 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.
 ,
, ,且
,且 ∥
∥ ,则
,则
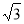 ;条件q:直线y= kx+2与圆x2+y2=1相切,则p是q的( )
;条件q:直线y= kx+2与圆x2+y2=1相切,则p是q的( )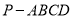 中,底面
中,底面 是矩形,
是矩形,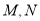 分别是
分别是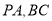 的中点,
的中点, 平面
平面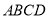 ,且
,且 ,
,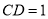 .
.
 平面
平面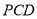 ;
;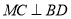 .
.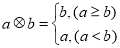 已知函数
已知函数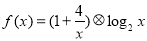 ,若函数
,若函数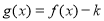 恰有两个零点,则
恰有两个零点,则 的取值范围为
的取值范围为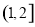 B.
B. 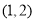 C.
C. 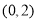 D.
D. 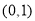
 ,且
,且 ,则
,则 = .
= .