题目内容
(2012•泰州二模)选修4-2:矩阵与变换
已知M=
,β=
,试计算M3β.
已知M=
|
|
分析:先根据特征值的定义列出特征多项式,令f(λ)=0解方程可得特征值,再由特征值列出方程组即可解得相应的特征向量,将矩阵β用征向量α1,α2,表示出来,然后再代入M3β进行计算.
解答:解:矩阵M的特征多项式为f(λ)=
=λ2-2λ-3
令f(λ)=0解得λ1=3,λ2=-1
从而矩阵M对应的特征向量分别为α1=
,α2=
令β=mα1+nα2,
所以m
+n
=
即
解得
故M3β=M3(4α1-3α2)
=4(M3α1)-3(M3α2)
=4(λ13α1)-3(λ23α2)
=4•33
-3(-1)3
=
|
令f(λ)=0解得λ1=3,λ2=-1
从而矩阵M对应的特征向量分别为α1=
|
|
令β=mα1+nα2,
所以m
|
|
|
即
|
|
故M3β=M3(4α1-3α2)
=4(M3α1)-3(M3α2)
=4(λ13α1)-3(λ23α2)
=4•33
|
|
|
点评:此部分是高中新增的内容,但不是很难,套用公式即可解答,主要考查学生的计算能力.

练习册系列答案
相关题目
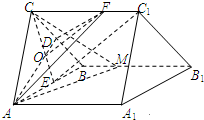 (2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.
(2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.