题目内容
若f(x)=2x2-lnx,则f(x)的单调减区间是________.
(0, )
)
分析:求出函数定义域,求导数f′(x),然后在定义域内解不等式f′(x)<0即可.
解答:f(x)的定义域为(0,+∞),
f′(x)=4x- =
=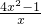 =
= ,
,
令f'(x)<0,解得0<x< ,
,
所以f(x)的单调减区间为(0, ).
).
故答案为:(0, ).
).
点评:本题考查利用导数研究函数的单调性,属基础题,准确求导,熟练解不等式是解决该类问题的基础.
 )
)分析:求出函数定义域,求导数f′(x),然后在定义域内解不等式f′(x)<0即可.
解答:f(x)的定义域为(0,+∞),
f′(x)=4x-
 =
=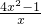 =
= ,
,令f'(x)<0,解得0<x<
 ,
,所以f(x)的单调减区间为(0,
 ).
).故答案为:(0,
 ).
).点评:本题考查利用导数研究函数的单调性,属基础题,准确求导,熟练解不等式是解决该类问题的基础.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
若f(x)=2x2-1(-
<x<
),f(a)=7,则a的值是( )
| 3 |
| 5 |
| A、1 | B、-1 | C、2 | D、±2 |