题目内容
(12分)已知函数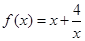
(1)试证明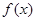 在
在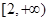 上为增函数;
上为增函数;
(2)当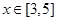 时,求函数
时,求函数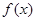 的最值
的最值
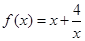
(1)试证明
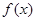 在
在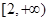 上为增函数;
上为增函数;(2)当
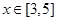 时,求函数
时,求函数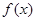 的最值
的最值(1)证明:见解析;
(2)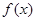 在
在 处取得最小值
处取得最小值 ,
,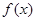 在
在 处取得最大值
处取得最大值
(2)
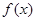 在
在 处取得最小值
处取得最小值 ,
,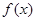 在
在 处取得最大值
处取得最大值
(1)根据单调性定义第一步在在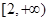 上任意取两个实数
上任意取两个实数 ,且
,且 ,
,
第二步作差比较 ,并且判定差值符号,第三步得出结论.
,并且判定差值符号,第三步得出结论.
(2)在(1)的基础上可知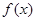 在区间
在区间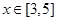 上是增函数,因而可知当x=3时,f(x)最小,当x=5时,f(x)最大.
上是增函数,因而可知当x=3时,f(x)最小,当x=5时,f(x)最大.
(1)证明:在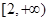 上任意取两个实数
上任意取两个实数 ,且
,且
∴

∵ ∴
∴

∴ 即
即
∴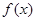 在
在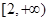 上为增函数;
上为增函数;
(2)∵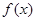 在
在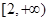 上为增函数
上为增函数
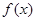 在
在 处取得最小值
处取得最小值
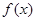 在
在 处取得最大值
处取得最大值
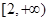 上任意取两个实数
上任意取两个实数 ,且
,且 ,
,第二步作差比较
 ,并且判定差值符号,第三步得出结论.
,并且判定差值符号,第三步得出结论.(2)在(1)的基础上可知
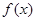 在区间
在区间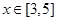 上是增函数,因而可知当x=3时,f(x)最小,当x=5时,f(x)最大.
上是增函数,因而可知当x=3时,f(x)最小,当x=5时,f(x)最大.(1)证明:在
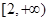 上任意取两个实数
上任意取两个实数 ,且
,且
∴


∵
 ∴
∴

∴
 即
即
∴
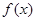 在
在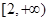 上为增函数;
上为增函数;(2)∵
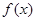 在
在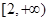 上为增函数
上为增函数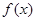 在
在 处取得最小值
处取得最小值
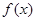 在
在 处取得最大值
处取得最大值

练习册系列答案
相关题目
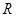 的函数
的函数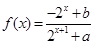 是奇函数
是奇函数 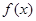 的解析式;
的解析式;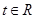 ,不等式
,不等式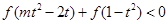 恒成立,求
恒成立,求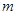 的取值范围.
的取值范围. 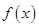 是定义在
是定义在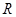 上单调函数,对任意实数
上单调函数,对任意实数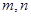 有:
有: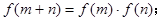 且
且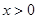 时,
时,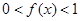 .
.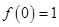 ;
;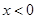 时,
时,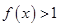 ;
;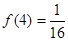 时,求使
时,求使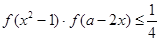 对任意实数
对任意实数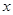 恒成立的参数
恒成立的参数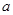 的取值范围.
的取值范围.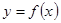 是定义在
是定义在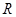 上的偶函数,且当
上的偶函数,且当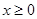 时,
时,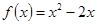 .
.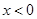 时,
时,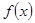 的解析式;
的解析式; ,则
,则 .
.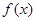 在
在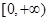 上是增函数,则满足
上是增函数,则满足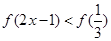 的
的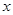 的取值范围是_____.
的取值范围是_____. 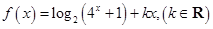 是偶函数.
是偶函数.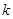 的值;
的值;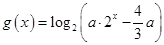 ,其中
,其中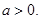 若函数
若函数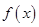 与
与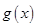 的图象有且只有一个交点,求
的图象有且只有一个交点,求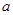 的取值范围.
的取值范围. ,则满足不等式
,则满足不等式 的
的 的取值范围
的取值范围



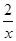 ;④f(x)=
;④f(x)=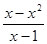 .
.