题目内容
(附加题)本小题满分10分
已知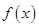 是定义在
是定义在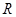 上单调函数,对任意实数
上单调函数,对任意实数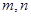 有:
有: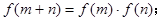 且
且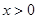 时,
时,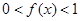 .
.
(1)证明: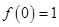 ;
;
(2)证明:当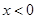 时,
时,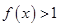 ;
;
(3)当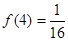 时,求使
时,求使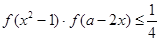 对任意实数
对任意实数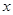 恒成立的参数
恒成立的参数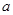 的取值范围.
的取值范围.
已知
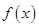 是定义在
是定义在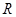 上单调函数,对任意实数
上单调函数,对任意实数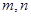 有:
有: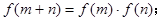 且
且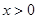 时,
时,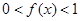 .
.(1)证明:
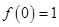 ;
;(2)证明:当
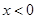 时,
时,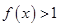 ;
;(3)当
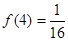 时,求使
时,求使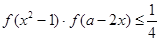 对任意实数
对任意实数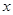 恒成立的参数
恒成立的参数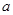 的取值范围.
的取值范围.解:(1)见解析;(2)见解析;(3)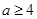 。
。
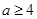 。
。本试题主要是考查了抽象函数的性质和解不等式的综合运用。
(1)在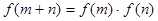 中,取
中,取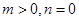 ,有
,有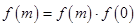 ,
,
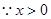 时,
时,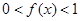 ,
, 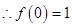
(2)设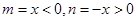 ,则
,则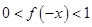 ,∴
,∴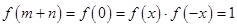
∴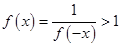 , 即
, 即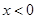 时,
时,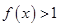
(3)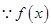 是定义在
是定义在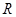 上单调函数,又
上单调函数,又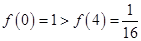
∴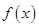 是定义域
是定义域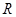 上的单调递减函数
上的单调递减函数
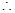 原不等式变为
原不等式变为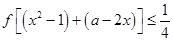 ,即
,即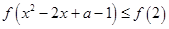
即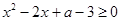 对任意实数
对任意实数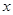 恒成立,结合判别式得到参数的范围。
恒成立,结合判别式得到参数的范围。
解:(1)在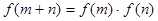 中,取
中,取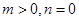 ,有
,有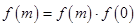 ,
,
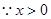 时,
时,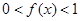 ,
, 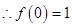 ……………2分
……………2分
(2)设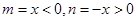 ,则
,则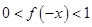 ,∴
,∴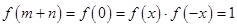
∴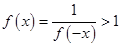 , 即
, 即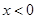 时,
时,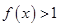 ……………5分
……………5分
(3)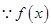 是定义在
是定义在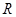 上单调函数,又
上单调函数,又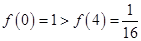
∴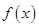 是定义域
是定义域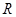 上的单调递减函数 ……………6分
上的单调递减函数 ……………6分
 ,且由已知
,且由已知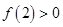 ,
,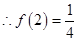 ……………7分
……………7分
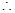 原不等式变为
原不等式变为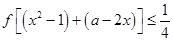 ,即
,即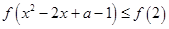 ……………8分
……………8分
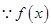 是定义域
是定义域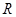 上的单调递减函数,可得,
上的单调递减函数,可得,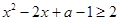 对任意实数
对任意实数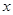 恒成立
恒成立
即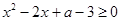 对任意实数
对任意实数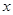 恒成立
恒成立
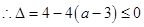 ,
,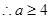 ……………10分
……………10分
(1)在
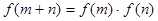 中,取
中,取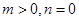 ,有
,有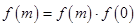 ,
,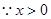 时,
时,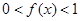 ,
, 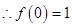
(2)设
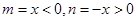 ,则
,则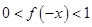 ,∴
,∴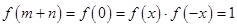
∴
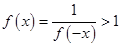 , 即
, 即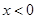 时,
时,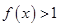
(3)
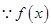 是定义在
是定义在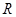 上单调函数,又
上单调函数,又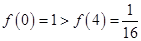
∴
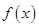 是定义域
是定义域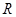 上的单调递减函数
上的单调递减函数 原不等式变为
原不等式变为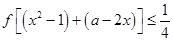 ,即
,即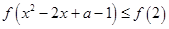
即
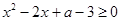 对任意实数
对任意实数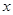 恒成立,结合判别式得到参数的范围。
恒成立,结合判别式得到参数的范围。解:(1)在
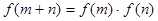 中,取
中,取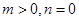 ,有
,有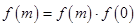 ,
,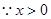 时,
时,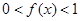 ,
, 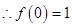 ……………2分
……………2分(2)设
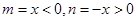 ,则
,则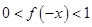 ,∴
,∴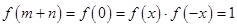
∴
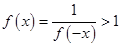 , 即
, 即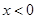 时,
时,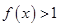 ……………5分
……………5分(3)
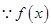 是定义在
是定义在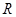 上单调函数,又
上单调函数,又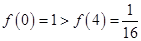
∴
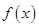 是定义域
是定义域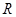 上的单调递减函数 ……………6分
上的单调递减函数 ……………6分 ,且由已知
,且由已知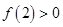 ,
,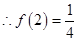 ……………7分
……………7分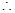 原不等式变为
原不等式变为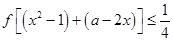 ,即
,即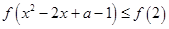 ……………8分
……………8分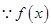 是定义域
是定义域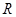 上的单调递减函数,可得,
上的单调递减函数,可得,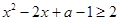 对任意实数
对任意实数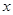 恒成立
恒成立即
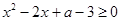 对任意实数
对任意实数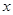 恒成立
恒成立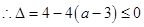 ,
,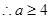 ……………10分
……………10分
练习册系列答案
 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
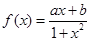 是定义域为
是定义域为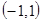 上的奇函数,且
上的奇函数,且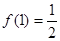
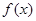 的解析式,
的解析式, 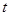 满足
满足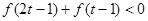 ,求实数
,求实数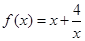
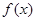 在
在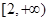 上为增函数;
上为增函数;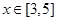 时,求函数
时,求函数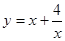
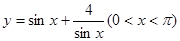
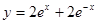
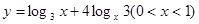
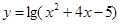 的单调递增区间为( )
的单调递增区间为( )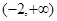
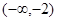
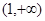
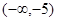
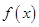 的定义域为A,若
的定义域为A,若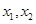
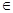 A,且
A,且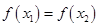 时总有
时总有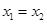 ,则称
,则称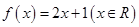 是单函数,下列命题:
是单函数,下列命题: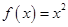
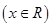 是单函数;
是单函数;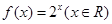 是单函数,
是单函数,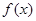 为单函数,
为单函数,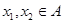 且
且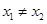 ,则
,则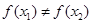 ;
;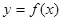 ,满足
,满足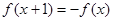 ,且在
,且在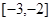 上是减函数,若
上是减函数,若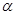 ,
,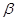 是锐角三角形的两个内角,则 ( )
是锐角三角形的两个内角,则 ( )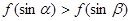


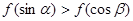
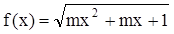 的定义域是一切实数,则m的取值范围是__________。
的定义域是一切实数,则m的取值范围是__________。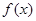 的定义域为R,当
的定义域为R,当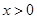 时,
时,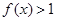 ,且对任意
,且对任意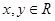 ,都有
,都有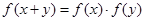 ,且
,且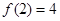 。
。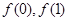 的值;
的值;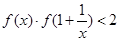 成立,求
成立,求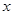 的取值范围。
的取值范围。