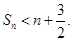题目内容
（12分）设函数
为奇函数，且
，数列
与
满足如下关系：
(1)求
的解析式；(2)求数列的通项公式
；（3）记
为数列的前
项和，求证：对任意的
有
(Ⅰ) 
(Ⅱ) 
（Ⅲ）略
解析:
：(1)由
是奇函数，得
，由
，得
故
(2)∵
∴
∴
，而
，∴
(3)证明：由(2) 
要证明的问题即为
当
时，
当
时，
∴
则
故
则
得证
练习册系列答案
相关题目
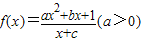为奇函数，且
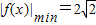，数列{an}与{bn}满足如下关系：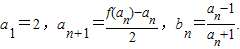
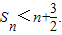
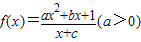为奇函数，且
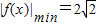，数列{an}与{bn}满足如下关系：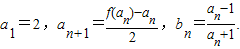
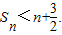
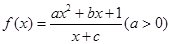为奇函数，且
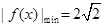，数列
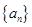与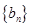
满足如下关系：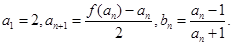
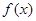的解析式；
；
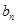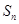为数列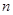
项和，求证：对任意的
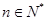有
为奇函数，且对任意
、
都有
，当
时
，求
上的最大值．