题目内容
13.设f(n)=($\frac{1+i}{1-i}$)n+($\frac{1-i}{1+i}$)n,n∈N,如果A⊆{f(n)},则满足条件的集合A有8个.分析 首先由复数代数形式的乘除运算化简$\frac{1+i}{1-i}$和$\frac{1-i}{1+i}$,然后根据虚数单位i的幂运算性质分类讨论,求出f(n)中的元素,则答案可求.
解答 解:∵$\frac{1+i}{1-i}=\frac{(1+i)^{2}}{(1-i)(1+i)}=\frac{2i}{2}=i$,
∴$\frac{1-i}{1+i}=-i$.
根据虚数单位i的幂运算性质有:f(n)=($\frac{1+i}{1-i}$)n+($\frac{1-i}{1+i}$)n=${i}^{n}+(-i)^{n}=\left\{\begin{array}{l}{2(n=4k,k∈Z)}\\{0(n=4k+1,k∈Z)}\\{-2(n=4k+2,k∈Z)}\\{0(n=4k+3,k∈Z)}\end{array}\right.$,
∴f(n)有三个不同的值,即f(n)=-2,0,2,A是{f(n)},它的一个子集.
∴A={-2},{0},{2},{-2,0},{0,2},{-2,2},2,0,2},{∅}.
则满足条件的集合A有8个.
故答案为:8.
点评 本题考查了复数代数形式的乘除运算,考查了分类讨论的思想方法,是中档题.

练习册系列答案
相关题目
5.对某种灯泡中随机地抽取200个样品进行使用寿命调查,结果如下:
规定:使用寿命大于或等于500天的灯泡是优等品,小于300天是次品,其余的是正品.某人从灯泡样品中随机地购买了n(n∈N*)个,如果这n个灯泡的等级分布情况恰好与从这200个样品中按三个等级分层抽样所得的结果相同,则n的最小值为( )
| 寿命(天) | 频数 | 频率 |
| [100,200) | 20 | 0.10 |
| [200,300) | 30 | y |
| [300,400) | 70 | 0.35 |
| [400,500) | x | 0.15 |
| [500,600) | 50 | 0.25 |
| 合计 | 200 | 1 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
2.已知a>0且a≠1,则使关于x的方程loga(x-2ak)=loga(x2-a2)有解的k的取值范围是( )
| A. | 0<k<$\frac{1}{2}$或k$<-\frac{1}{2}$ | B. | 0<k<1或k<-1 | C. | 0<k<2或k<-2 | D. | 0<k<1或k<-2 |
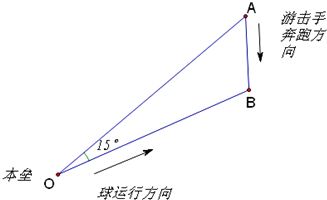 在奥运会垒球比赛前,C国教练布置战术时,要求击球手以与连结本垒及游击手的直线成15°的方向把球击出,根据经验及测速仪的显示,通常情况下球速为游击手最大跑速的4倍,问按这样的布置,游击手能不能接着球?(如图所示)
在奥运会垒球比赛前,C国教练布置战术时,要求击球手以与连结本垒及游击手的直线成15°的方向把球击出,根据经验及测速仪的显示,通常情况下球速为游击手最大跑速的4倍,问按这样的布置,游击手能不能接着球?(如图所示)