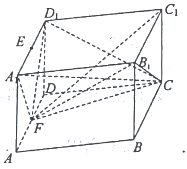
题目内容
【题目】已知椭圆C: ![]() 的右焦点为F(1,0),且点(﹣1,
的右焦点为F(1,0),且点(﹣1, ![]() )在椭圆C上.
)在椭圆C上.
(1)求椭圆C的标准方程;
(2)已知动直线l过点F,且与椭圆C交于A,B两点,试问x轴上是否存在定点Q,使得 ![]() 恒成立?若存在,求出点Q的坐标,若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标,若不存在,请说明理由.
【答案】
(1)解:由题意,c=1
∵点(﹣1, ![]() )在椭圆C上,∴根据椭圆的定义可得:2a=
)在椭圆C上,∴根据椭圆的定义可得:2a= ![]() ,∴a=
,∴a= ![]()
∴b2=a2﹣c2=1,
∴椭圆C的标准方程为 ![]()
(2)解:假设x轴上存在点Q(m,0),使得 ![]() 恒成立
恒成立
当直线l的斜率为0时,A( ![]() ,0),B(﹣
,0),B(﹣ ![]() ,0),则
,0),则 ![]() =﹣
=﹣ ![]() ,∴
,∴ ![]() ,∴m=
,∴m= ![]() ①
①
当直线l的斜率不存在时, ![]() ,
, ![]() ,则
,则 ![]()
![]() =﹣
=﹣ ![]() ,
,
∴ ![]()
∴m= ![]() 或m=
或m= ![]() ②
②
由①②可得m= ![]() .
.
下面证明m= ![]() 时,
时, ![]() 恒成立
恒成立
当直线l的斜率为0时,结论成立;
当直线l的斜率不为0时,设直线l的方程为x=ty+1,A(x1,y1),B(x2,y2)
直线方程代入椭圆方程,整理可得(t2+2)y2+2ty﹣1=0,∴y1+y2=﹣ ![]() ,y1y2=﹣
,y1y2=﹣ ![]()
∴ ![]() =(x1﹣
=(x1﹣ ![]() ,y1)(x2﹣
,y1)(x2﹣ ![]() ,y2)=(ty1﹣
,y2)=(ty1﹣ ![]() )(ty2﹣
)(ty2﹣ ![]() )+y1y2=(t2+1)y1y2﹣
)+y1y2=(t2+1)y1y2﹣ ![]() t(y1+y2)+
t(y1+y2)+ ![]() =
= ![]() +
+ ![]() =﹣
=﹣ ![]()
综上,x轴上存在点Q( ![]() ,0),使得
,0),使得 ![]() 恒成立
恒成立
【解析】(1)利用椭圆的定义求得a的值,进而求得b的值,即可求得椭圆的方程;(2)先假设点Q存在,进而求得此时m的值,再证明m取该值时所给的关于向量的等式成立.
【考点精析】利用椭圆的标准方程对题目进行判断即可得到答案,需要熟知椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.

【题目】某公司为了研究年宣传费![]() (单位:千元)对销售量
(单位:千元)对销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:千元)的影响,搜集了近 8 年的年宣传费
(单位:千元)的影响,搜集了近 8 年的年宣传费![]() 和年销售量
和年销售量![]() 数据:
数据:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 38 | 40 | 44 | 46 | 48 | 50 | 52 | 56 |
| 45 | 55 | 61 | 63 | 65 | 66 | 67 | 68 |
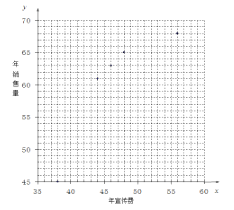
(Ⅰ)请补齐表格中 8 组数据的散点图,并判断![]() 与
与![]() 中哪一个更适宜作为年销售量
中哪一个更适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的函数表达式?(给出判断即可,不必说明理由)
的函数表达式?(给出判断即可,不必说明理由)
(Ⅱ)若(Ⅰ)中的![]() ,且产品的年利润
,且产品的年利润![]() 与
与![]() ,
, ![]() 的关系为
的关系为![]() ,为使年利润值最大,投入的年宣传费 x 应为何值?
,为使年利润值最大,投入的年宣传费 x 应为何值?