题目内容
7．如图，菱形ABCD的边长为2，∠A=60°，M为DC的中点，则$\overrightarrow{AM}$•$\overrightarrow{AB}$的值为4．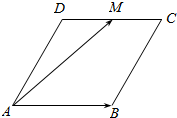
分析 建立适当的坐标系，如图所示，找出M与B坐标，利用平面向量的数量积运算法则即可确定出所求式子的值．
解答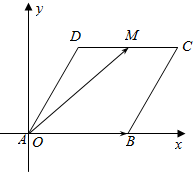 
解：建立平面直角坐标系，如图所示，
∵菱形ABCD的边长为2，∠A=60°，M为DC的中点，
∴D（1，$\sqrt{3}$），C（3，$\sqrt{3}$），
∴线段CD中点M坐标为（2，$\sqrt{3}$），
∴$\overrightarrow{OM}$=（2，$\sqrt{3}$），$\overrightarrow{OB}$=（2，0），
则$\overrightarrow{AM}$•$\overrightarrow{AB}$=4．
故答案为：4．
点评 此题考查了平面向量数量积的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
已知全集U=R，集合M={x|-1≤x≤3}和N={x|x=2k-1，k=1，2，…}的关系的韦恩（Venn）图如图所示，则阴影部分所示的集合的元素共有2个．
12．若x∈（1，e），a=ln x，b=（ln x）2，c=ln（ln x），则a，b，c的大小关系为（ ）
| A． | c＞b＞a | B． | b＞c＞a | C． | a＞b＞c | D． | b＞a＞c |
16．已知函数f（x）=$\left\{\begin{array}{l}{2x-1，-1＜x≤2}\\{{x}^{2}-2，2＜x＜3}\end{array}\right.$，则不等式f（x）＞x的解集为（ ）
| A． | （1，3） | B． | （-∞，1）∪（3，+∞） | C． | {2} | D． | （1，2）∪（2，3） |