题目内容
若关于x的方程:9x+(4+a)•3x+4=0有解,则实数a的取值范围为( )A.(-∞,-8)∪[0,+∞)
B.(-8,-4)
C.[-8,-4]
D.(-∞,-8]
【答案】分析:可分离出a+4,转化为函数f(x)=- 的值域问题,令3x=t,利用基本不等式和不等式的性质求值域即可.
的值域问题,令3x=t,利用基本不等式和不等式的性质求值域即可.
解答:解:∵a+4=- ,
,
令3x=t(t>0),则- =-
=-
因为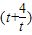 ≥4,所以-
≥4,所以- ≤-4,
≤-4,
∴a+4≤-4,
所以a的范围为(-∞,-8]
故选D.
点评:本题考查指数函数的定义、解析式、定义域和值域、方程有解问题、基本不等式求最值问题,同时考查转化思想和换元法.
 的值域问题,令3x=t,利用基本不等式和不等式的性质求值域即可.
的值域问题,令3x=t,利用基本不等式和不等式的性质求值域即可.解答:解:∵a+4=-
 ,
,令3x=t(t>0),则-
 =-
=-
因为
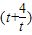 ≥4,所以-
≥4,所以- ≤-4,
≤-4,∴a+4≤-4,
所以a的范围为(-∞,-8]
故选D.
点评:本题考查指数函数的定义、解析式、定义域和值域、方程有解问题、基本不等式求最值问题,同时考查转化思想和换元法.

练习册系列答案
相关题目
若关于x的方程:9x+(4+a)•3x+4=0有解,则实数a的取值范围为( )
| A、(-∞,-8)∪[0,+∞) | B、(-8,-4) | C、[-8,-4] | D、(-∞,-8] |