题目内容
3.在曲线C上的动点P(a,a2+2a)与动点Q(b,b2+2b)(a<b<0)的切线互相垂直,则b-a最小值为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | -$\sqrt{2}$ |
分析 由题意可得曲线y=x2+2x上存在两点处的切线互相垂直,求出函数y=x2+2x的导数,结合两直线垂直的条件:斜率之积为-1,可得b-a=$\frac{1}{-4(a+1)}$+(-a-1),(a+1<0),运用基本不等式即可得到所求最小值.
解答 解:由题意可得曲线y=x2+2x上存在两点处的切线互相垂直,
由y=x2+2x的导数为y′=2x+2,
可得(2a+2)(2b+2)=-1,
由a+1<b+1,可得a+1<0,
且b=$\frac{1}{-4(a+1)}$,b-a=$\frac{1}{-4(a+1)}$+(-a-1)≥2$\sqrt{(-a-1)•\frac{1}{-4(a+1)}}$=2×$\frac{1}{2}$=1,
当且仅当$\frac{1}{-4(a+1)}$=(-a-1),解得a=-$\frac{3}{2}$,可得b-a的最小值为1.
故选:A.
点评 本题考查导数的运用:求切线的斜率,考查基本不等式的运用:求最值,化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
3.已知向量$\vec a$、$\vec b$满足$({\vec a+2\vec b})•({\vec a-\vec b})=-6$,且$|{\vec a}|=1$,$|{\vec b}|=2$,则$\vec a$与$\vec b$的夹角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
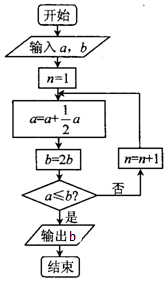 宋元时期数学名著《算学启蒙》中关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的b=( )
宋元时期数学名著《算学启蒙》中关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的b=( )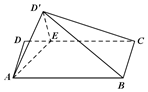 如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.
如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.