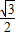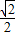题目内容
椭圆的一焦点与短轴两顶点组成一个等边三角形,则椭圆的离心率为 .
分析:根据题意,作出示意图,可得△ABF2为等边三角形,即|OF2|=
|AB|,可得c=
b,由此结合b2=a2-c2即可解出椭圆的离心率为
.
| ||
| 2 |
| 3 |
| ||
| 2 |
解答:解:设椭圆的焦点分别为F1、F2,上顶点为B,下顶点为A,如图所示
∵一焦点与短轴两顶点组成一个等边三角形,即△ABF2为等边三角形
∴|OF2|=
|AB|,可得c=
b
平方得c2=3b2=3(a2-c2),所以3a2=4c2,
可得e2=
=
,得e=
故答案为:

∵一焦点与短轴两顶点组成一个等边三角形,即△ABF2为等边三角形
∴|OF2|=
| ||
| 2 |
| 3 |
平方得c2=3b2=3(a2-c2),所以3a2=4c2,
可得e2=
| c2 |
| a2 |
| 3 |
| 4 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题给出椭圆的一个焦点与短轴构成正三角形,求椭圆的离心率,着重考查了正三角形的性质、椭圆的标准方程与简单几何性质等知识,属于基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
椭圆的一焦点与短轴两顶点组成一个等边三角形,则椭圆的离心率e=
为( )
| c |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 为( )
为( )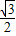

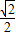

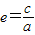 为( )
为( )