题目内容
已知向量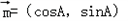 ,
,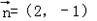 ,且
,且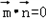 .
.
(1)求tanA的值;
(2)求函数f(x)=cos2x+tanAsinx(x∈R)的值域.
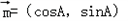 ,
,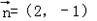 ,且
,且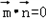 .
.(1)求tanA的值;
(2)求函数f(x)=cos2x+tanAsinx(x∈R)的值域.
解:(1)由题意得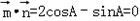 ,
,
因为cosA≠0,所以tanA=2.
(2)由(1)知tanA=2得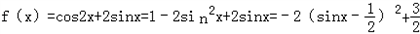 .
.
因为x∈R,所以sinx∈[﹣1,1].
当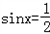 时,f(x)有最大值
时,f(x)有最大值 ;
;
当sinx=﹣1时,f(x)有最小值﹣3;
故所求函数f(x)的值域是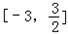 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
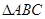 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为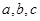 ,已知向量
,已知向量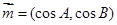 ,
,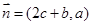 ,且
,且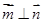 。
。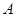 的大小;
的大小; 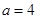 ,求
,求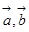 满足
满足 ,且
,且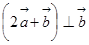 .
.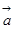 的坐标; (2)、求向量
的坐标; (2)、求向量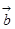 的夹角.
的夹角. ,
, ,且
,且 .
. 及
及 ;
;
 的最小值是
的最小值是 ,求实数
,求实数 的值.
的值.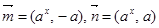 ,其中
,其中 且
且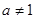 ,
,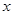 为何值时,
为何值时,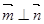 ;
;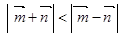 .
. ,其中
,其中 且
且 ,
, 为何值时,
为何值时, ;
; .
.