题目内容
已知△ABC为等边三角形,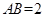 ,设点P,Q满足
,设点P,Q满足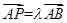 ,
, ,
,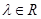 ,若
,若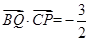 ,则
,则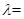
A.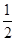 | B.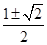 | C. | D. |
A
解析试题分析:∵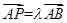 ,
, ,λ∈R
,λ∈R
∴ ,
, ,
,
∵△ABC为等边三角形,AB=2
∴
=2×2×cos60°+λ×2×2×cos180°+(1-λ)×2×2×cos180°+λ(1-λ)×2×2×cos60°=-2λ2+2λ+2,
∵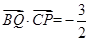 ,
,
∴4λ2-4λ+1=0
∴(2λ-1)2=0
∴λ=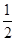
故选A。
考点:平面向量的线性运算,平面向量的数量积。
点评:中档题,解题的关键是根据向量加法的三角形法则求出 的表达形式,以进一步建立λ的方程。
的表达形式,以进一步建立λ的方程。

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
已知平面向量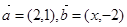 ,且
,且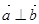 ,则
,则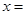 ( )
( )
| A.-3 | B.3 | C.-1 | D.1 |
已知向量 ,
, ,若
,若 ,则实数
,则实数 的值为( ).
的值为( ).
A. | B. | C. | D. |
已知a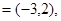 b=
b=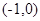 ,向量
,向量 垂直,则实数
垂直,则实数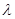 的值为( )
的值为( )
A.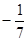 | B.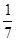 | C.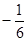 | D.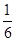 |
在四边形ABCD中,若 ,且
,且 ,则( )
,则( )
| A.ABCD是矩形 | B.ABCD是正方形 |
| C.ABCD是菱形 | D.ABCD是平行四边形 |
已知向量满足 ,满足
,满足 ,
, ,若
,若 与
与 共线,则
共线,则 的最小值为( )
的最小值为( )
A.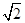 | B. | C. | D. |
向量 在向量
在向量 上的投影是( )
上的投影是( )
A. | B. | C. | D. |
 满足
满足 ,其中k>0,记函数f(
,其中k>0,记函数f(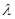 )=
)= ,
, ,当f(
,当f( 垂直的向量可以是
垂直的向量可以是 



 的两条直角边
的两条直角边
 两点分别在
两点分别在 轴、
轴、 轴的正半轴(含原点)上滑动,
轴的正半轴(含原点)上滑动, 分别为
分别为 的中点.则
的中点.则 的最大值是
的最大值是


