题目内容
已知当x
R时，不等式a+cos2x<5
4sinx+
恒成立，求实数a的取值范围。
【答案】
解：原不等式即：4sinx+cos2x<
a+5
要使上式恒成立，只需a+5大于4sinx+cos2x的最大值，故上述问题转化成求f(x)=4sinx+cos2x的最值问题。
f(x)= 4sinx+cos2x=2sin2x+4sinx+1=2(sinx1)2+3
3,
∴a+5>3即>a–2
上式等价于
或
，解得
a<8
练习册系列答案
期末集结号系列答案
相关题目
．
R恒成立，求f(x)的单调递减区间．
．
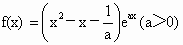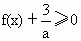对任意x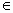
R恒成立，求a的取值范围．
R时，不等式a+cos2x<5
4sinx+
恒成立，求实数a的取值范围。