题目内容
已知f(x)=log2x,当点M(x,y)在y=f(x)的图象上运动时,点N(x,ny)在函数y=gn(x)的图象上运动(n∈N).
(1)求y=gn(x)的解析式;
(2)求集合A={a|关于x的方程g1(x+2)=g2(x+a)有实根,a∈R};
(3)设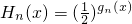 ,函数F(x)=H1(x)-g1(x),(0<a≤x≤b)的值域为
,函数F(x)=H1(x)-g1(x),(0<a≤x≤b)的值域为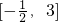 ,
,
求证: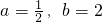 .
.
解:(1)由条件知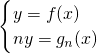 ,又f(x)=log2x∴解析式gn(x)=nlog2x.
,又f(x)=log2x∴解析式gn(x)=nlog2x.
(2)∵方程g1(x+2)=g2(x+a),即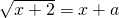 ,
,
∴求集合A就是求方程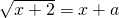 有实根时a的范围.
有实根时a的范围.
而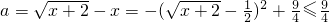 ,
,
∴ 时原方程总有实根,
时原方程总有实根,
∴集合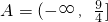 .
.
(3)∵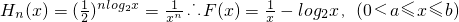 ,
,
又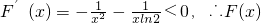 在[a,b]上递减,
在[a,b]上递减,
∴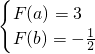 ,即
,即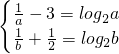 ①,
①,
由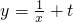 与y=log2x的图象只有唯一交点知:方程
与y=log2x的图象只有唯一交点知:方程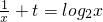 只有唯一解,
只有唯一解,
经检验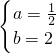 是方程组①的唯一解,故得证.
是方程组①的唯一解,故得证.
分析:(1)由于f(x)=log2x,点N(x,ny)又在函数y=gn(x)的图象上运动(n∈N).所以,直接代入即可;
(2)关于x的方程g1(x+2)=g2(x+a)有实根,即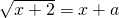 有实根,实质是求函数y=
有实根,实质是求函数y= 的值域;
的值域;
(3)函数F(x)=H1(x)-g1(x),(0<a≤x≤b)的值域为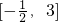 ,故此,本问题只需判断出函数F(x)在[a,b]上的单调性即可求解a,b.
,故此,本问题只需判断出函数F(x)在[a,b]上的单调性即可求解a,b.
点评:待定系数法是求函数解析式的一种常见方法,例如问题(1);转化思想是数学中的重要思想之一,问题的转化往往可以收到意想不到的效果,如问题(2);问题(3)再次展现了求解函数最值时导数的工具性作用.
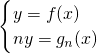 ,又f(x)=log2x∴解析式gn(x)=nlog2x.
,又f(x)=log2x∴解析式gn(x)=nlog2x.(2)∵方程g1(x+2)=g2(x+a),即
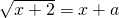 ,
,∴求集合A就是求方程
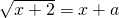 有实根时a的范围.
有实根时a的范围.而
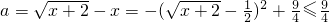 ,
,∴
 时原方程总有实根,
时原方程总有实根,∴集合
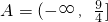 .
.(3)∵
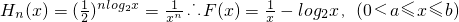 ,
,又
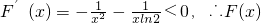 在[a,b]上递减,
在[a,b]上递减,∴
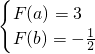 ,即
,即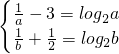 ①,
①,由
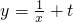 与y=log2x的图象只有唯一交点知:方程
与y=log2x的图象只有唯一交点知:方程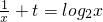 只有唯一解,
只有唯一解,经检验
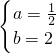 是方程组①的唯一解,故得证.
是方程组①的唯一解,故得证.分析:(1)由于f(x)=log2x,点N(x,ny)又在函数y=gn(x)的图象上运动(n∈N).所以,直接代入即可;
(2)关于x的方程g1(x+2)=g2(x+a)有实根,即
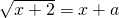 有实根,实质是求函数y=
有实根,实质是求函数y= 的值域;
的值域;(3)函数F(x)=H1(x)-g1(x),(0<a≤x≤b)的值域为
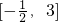 ,故此,本问题只需判断出函数F(x)在[a,b]上的单调性即可求解a,b.
,故此,本问题只需判断出函数F(x)在[a,b]上的单调性即可求解a,b.点评:待定系数法是求函数解析式的一种常见方法,例如问题(1);转化思想是数学中的重要思想之一,问题的转化往往可以收到意想不到的效果,如问题(2);问题(3)再次展现了求解函数最值时导数的工具性作用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知f(x)是定义在R上的奇函数,当x>0时,f(x)=log
x,那么f(-
)的值是( )
| 1 |
| 4 |
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |