题目内容
已知向量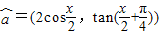 ,
,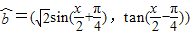 ,令f(x)=
,令f(x)=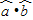
(1)求函数f(x)的最小正周期,并写出f(x)在[0,π]上的单调递增区间.
(2)若f(x)=-
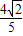 且
且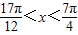 ,求
,求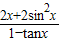 的值.
的值.
【答案】分析:(1)利用两个向量的数量积公式,两角和差的三角公式,同角三角函数的基本关系,化简函数f(x)的解析式为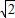 sin(x+
sin(x+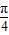 ),可得函数的最小正周期等于2π,在[0,
),可得函数的最小正周期等于2π,在[0,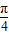 ]上的单调递增.
]上的单调递增.
(2)由f(x)=-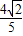 ,可得sin(x+
,可得sin(x+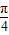 ) 的值,从而求得 tan(x+
) 的值,从而求得 tan(x+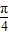 ) 的值,由
) 的值,由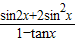 =[1-2
=[1-2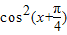 ]•tan(x+
]•tan(x+ ) 求出结果.
) 求出结果.
解答:解:(1)函数f(x)=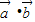 =2
=2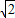 cos
cos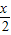 sin(
sin(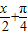 )+tan(
)+tan(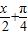 )tan(
)tan(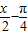 )
)
=2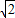 cos
cos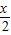 (
( +
+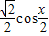 )+
)+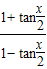 •
•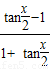 =2sin
=2sin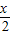 cos
cos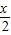 +2
+2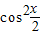 -1
-1
=sinx+cosx= sin(x+
sin(x+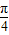 ),故函数的最小正周期等于2π,f(x)在[0,
),故函数的最小正周期等于2π,f(x)在[0,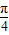 ]上的单调递增.
]上的单调递增.
(2)若f(x)=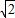 sin(x+
sin(x+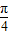 )=-
)=-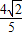 ,∴sin(x+
,∴sin(x+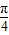 )=
)=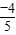 ,由
,由 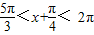 ,
,
∴cos(x+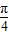 )=
)= ,∴tan(x+
,∴tan(x+ )=
)=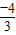 ,
,
∴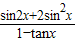 =sin2x•
=sin2x•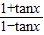 =-cos(2x+
=-cos(2x+ )•tan(x+
)•tan(x+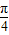 )=[1-2
)=[1-2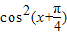 ]•tan(x+
]•tan(x+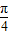 )
)
=[1-2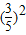 ]•(-
]•(- )=-
)=-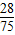 .
.
点评:本题考查两个向量的数量积公式,两角和差的三角公式,同角三角函数的基本关系,式子的变形是解题的关键.
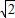 sin(x+
sin(x+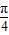 ),可得函数的最小正周期等于2π,在[0,
),可得函数的最小正周期等于2π,在[0,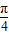 ]上的单调递增.
]上的单调递增.(2)由f(x)=-
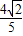 ,可得sin(x+
,可得sin(x+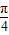 ) 的值,从而求得 tan(x+
) 的值,从而求得 tan(x+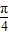 ) 的值,由
) 的值,由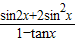 =[1-2
=[1-2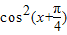 ]•tan(x+
]•tan(x+ ) 求出结果.
) 求出结果.解答:解:(1)函数f(x)=
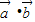 =2
=2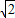 cos
cos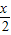 sin(
sin(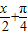 )+tan(
)+tan(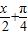 )tan(
)tan(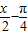 )
) =2
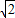 cos
cos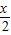 (
( +
+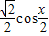 )+
)+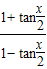 •
•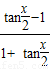 =2sin
=2sin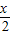 cos
cos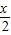 +2
+2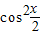 -1
-1 =sinx+cosx=
 sin(x+
sin(x+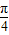 ),故函数的最小正周期等于2π,f(x)在[0,
),故函数的最小正周期等于2π,f(x)在[0,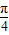 ]上的单调递增.
]上的单调递增.(2)若f(x)=
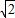 sin(x+
sin(x+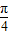 )=-
)=-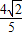 ,∴sin(x+
,∴sin(x+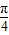 )=
)=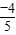 ,由
,由 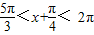 ,
,∴cos(x+
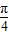 )=
)= ,∴tan(x+
,∴tan(x+ )=
)=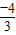 ,
,∴
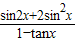 =sin2x•
=sin2x•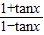 =-cos(2x+
=-cos(2x+ )•tan(x+
)•tan(x+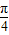 )=[1-2
)=[1-2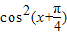 ]•tan(x+
]•tan(x+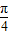 )
) =[1-2
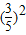 ]•(-
]•(- )=-
)=-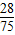 .
.点评:本题考查两个向量的数量积公式,两角和差的三角公式,同角三角函数的基本关系,式子的变形是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
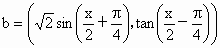 ,令
,令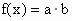 ,是否存在实数x∈[0,π],使
,是否存在实数x∈[0,π],使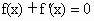 (其中
(其中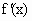 是f(x)的导函数)?若存在,则求出x的值;若不存在,则证明.
是f(x)的导函数)?若存在,则求出x的值;若不存在,则证明.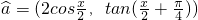 ,
,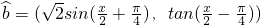 ,令f(x)=
,令f(x)=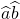
 且
且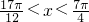 ,求
,求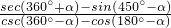 的值.
的值.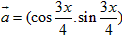 ,
,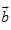 =
=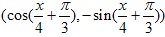 ,令
,令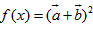 。
。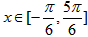 ,求函数f(x)的最大值和最小值。
,求函数f(x)的最大值和最小值。