题目内容

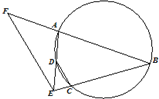如图，A，B，C，D四点在同一圆上，BC与AD的延长线交于点E，点F在BA的延长线上，若
EC
EB
=
1
3
，
ED
EA
=
1
2
，则
DC
AB
的值为
 
．
考点：与圆有关的比例线段
专题：立体几何
分析：由已知得△ECD∽△EAB，
DC
AB
=
EC
AE
=
DE
BE
=
1
3
BE
2DE
，从而BE=
6
DE，由此能求出
DC
AB
=
DE
BE
=
DE
6
DE
=
6
6
．
解答： 解：∵A，B，C，D四点共圆
∴∠EDC=∠EBF，
又∵∠DEC=∠AEC 
∴△ECD∽△EAB，
又∵
EC
EB
=
1
3
，
ED
EA
=
1
2
，
∴
DC
AB
=
EC
AE
=
DE
BE
=
1
3
BE
2DE
，
∴BE2=6DE2，即BE=
6
DE，
∴
DC
AB
=
DE
BE
=
DE
6
DE
=
6
6
．
故答案为：
6
6
．
点评：本题考查两线段长的比值的求法，是中档题，解题时要注意圆的性质的合理运用．
练习册系列答案
相关题目
函数f（x）=3sinx-log 
1
2
x零点的个数为
 
．
已知实数x，y满足
x≥1
x+y≤4
ax+by+c≤0
，且目标函数z=2x+y的最大值为6，最小值为1（其中b≠0），则
c
b
的值为
 
．
求函数y=cos（2x+
π
3
）图象的一个对称中心．
已知函数f（x）是奇函数，且当x＞0时，f（x）=x（2-x），求x＜0时，f（x）的解析式．
设函数f（x）=-x（x-a）2（x∈R），其中a∈R．
（1）当a=1时，求曲线y=f（x）在点（2，f（2））处的切线方程；
（2）当a≠0时，求函数f（x）的极大值和极小值；
（3）当a=3时，函数图象与直线y=m有三个交点，求实数m的取值范围．
已知函数f（x）=xlnx-x．
（1）求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）求函数f（x）的极值．
已知函数f（x）=x-alnx（a∈R）
（1）当a=2时，求曲线y=f（x）在点A（1，f（1））处的切线方程；
（2）讨论函数f（x）的单调性与极值；
（3）当a=2时，求函数f（x）在[1，3]上的最值．
已知元素为正整数的数集序列{1}，{2，3}，{4，5，6}，{7，8，9，10}，…从第二个数集开始，每一个数集比前一个数集多一个元素，且每一个数集中最小的元素比前一个数集中最大的元素大1，则第n个数集中所有元素之和Sn=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网