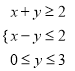题目内容
【题目】设函数![]() ,
, ![]() .
.
(Ⅰ)若曲线![]() 与曲线
与曲线![]() 在它们的交点
在它们的交点![]() 处具有公共切线,求
处具有公共切线,求![]() ,
, ![]() 的值;
的值;
(Ⅱ)当![]() 时,若函数
时,若函数![]() 在区间
在区间![]() 内恰有两个零点,求
内恰有两个零点,求![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 上的最大值.
上的最大值.
【答案】(1)![]() ,
, ![]() .(2)
.(2)![]() (3)见解析
(3)见解析
【解析】【试题分析】(1)借助导数的几何意义建立方程组求解;(2)依据题设条件借助到数与函数的单调性之间的关系分析求解;(3)借助题设条件运用分类整合思想进行分析求解:
(Ⅰ)![]() ,
, ![]() .
.
因为曲线![]() 与曲线
与曲线![]() 在它们的交点
在它们的交点![]() 处具有公共切线,所以
处具有公共切线,所以![]() ,且
,且![]() ,即
,即![]() ,且
,且![]() ,解得
,解得![]() ,
, ![]() .
.
(Ⅱ)记![]() ,当
,当![]() 时,
时, ![]() ,
,
![]() ,令
,令![]() ,得
,得![]() ,
, ![]() ,
,
当![]() 变化时,
变化时, ![]() ,
, ![]() 的变化情况如表:
的变化情况如表:
|
|
|
|
|
|
所以函数![]() 的单调增区间为
的单调增区间为![]() ,
, ![]() ;单调减区间为
;单调减区间为![]() .
.
故![]() 在区间
在区间![]() 内单调递增,在区间
内单调递增,在区间![]() 内单调递减,
内单调递减,
从而函数![]() 在区间
在区间![]() 内恰有两个零点,当且仅当
内恰有两个零点,当且仅当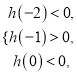 解得
解得![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)记![]() ,当
,当![]() 时,
时, ![]() ,
,
由(Ⅱ)![]() 的单调增区间为
的单调增区间为![]() ,
, ![]() ;单调减区间为
;单调减区间为![]() .
.
①当![]() 时,即
时,即![]() 时,
时, ![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以![]() 在区间
在区间![]() 上的最大值为
上的最大值为
![]() ;
;
②当![]() 且
且![]() ,即
,即![]() 时,
时, ![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,所以
上单调递减,所以![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ;
;
当![]() 且
且![]() ,即
,即![]() 时,
时, ![]() 且
且![]() ,所以
,所以![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ;
;
③当![]() 时,
时, ![]() ,
, ![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,所以
上单调递增,所以![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() 与
与![]() 中的较大者,
中的较大者,
由![]() 知,当
知,当![]() 时,
时, ![]() ,所以
,所以![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ;
;
④当![]() 时,
时, ![]() 在区间
在区间![]() 上单调递增,所以
上单调递增,所以![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() .
.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
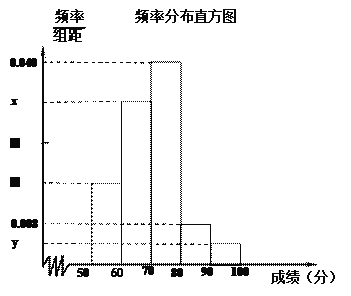
英才计划同步课时高效训练系列答案【题目】我校举行的 “青年歌手大选赛”吸引了众多有才华的学生参赛.为了了解本次比赛成绩情况,从中抽取了50名学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
![]()
组别 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 8 | 0.16 |
第2组 | [60,70) | a | ▓ |
第3组 | [70,80) | 20 | 0.40 |
第4组 | [80,90) | ▓ | 0.08 |
第5组 | [90,100] | 2 | b |
合计 | ▓ | ▓ |
(1)求出![]() 的值;
的值;
(2)在选取的样本中,从成绩是80分以上(含80分)的同学中随机抽取2名同学参加元旦晚会,求所抽取的2名同学中至少有1名同学来自第5组的概率;
(3)根据频率分布直方图,估计这50名学生成绩的众数、中位数和平均数。