题目内容
17．函数f（x）=$\frac{1}{x-1}$+lg（x+1）的定义域为（ ）| A． | （-∞，-1） | B． | （1，+∞） | C． | （-1，1）∪（1，+∞） | D． | R |
分析 由分式的分母不为0，对数式的真数大于0联立不等式组得答案．
解答 解：由$\left\{\begin{array}{l}{x-1≠0}\\{x+1＞0}\end{array}\right.$，解得x＞-1且x≠1．
∴函数f（x）=$\frac{1}{x-1}$+lg（x+1）的定义域为（-1，1）∪（1，+∞）．
故选：C．
点评 本题考查函数的定义域及其求法，考查了不等式组的解法，是基础题．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
7．直线y=$\frac{1}{2}$与曲线y=2sin（x+$\frac{π}{2}$）cos（x-$\frac{π}{2}$）在y轴右侧的交点自左向右依次记为M1，M2，M3，…，则$\overrightarrow{|{M_1}{M_{13}}}$|等于（ ）
| A． | 6π | B． | 7π | C． | 12π | D． | 13π |
9．如图，在矩形 OABC中，$\overrightarrow{{A}{B}}=3\overrightarrow{{A}{E}}$，$\overrightarrow{{B}C}=3\overrightarrow{FC}$，若$\overrightarrow{{O}{B}}=λ\overrightarrow{{O}{E}}+μ\overrightarrow{{O}F}$（λ，μ∈R），则λμ等于（ ）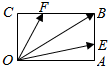
| A． | $\frac{9}{4}$ | B． | $\frac{9}{16}$ | C． | $\frac{4}{9}$ | D． | $\frac{16}{9}$ |
7．已知f（x）=log2x，则f-1（x）满足（ ）
| A． | f-1（2x）=2f-1（x） | B． | f-1（2x）=$\frac{1}{2}$f-1（x） | C． | f-1（2x）=[f-1（x）]2 | D． | f-1（2x）=[f-1（x）]${\;}^{\frac{1}{2}}$ |