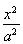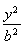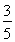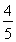题目内容
设椭圆
2=1(a＞b＞0)的右焦点为F，斜率为1的直线l过点F，交椭圆于A、B两点，O为坐标原点.已知椭圆上存在一点C使
+
=
.（1）求椭圆的离心率;
（2）若|
|=15，求椭圆的方程.
解析：（1）直线l方程为y=x-c代入=1(a＞b＞0)，得（a2+b2）x2-2a2cx+a2c2-a2b2=0.设A（x1,y1）,B(x2,y2)，
则x1+x2=,y1+y2=-
∵=+
，
∴C点的坐标为（
,-
）.
∵C在椭圆上，∴
=1，即
=1.
∴4c2=a2+b2,∴5c2=2a2.∴e=
.
（2）∵|AB|=|AF|+|BF|=(a-ex1)+(a-ex2)=2a-e(x1+x2)=2a-
.
已知
a=15,
∴a=10,e=
,a=2
.∴b2=60.
∴椭圆方程为
=1.
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
=1(a＞b＞0)过点(1,
),F1、F2分别为椭圆C的左、右两个焦点，且离心率e=
.
,求直线l的方程；
=1(a＞b＞0)过点(1,
),F1、F2分别为椭圆C的左、右两个焦点,且离心率e=
.
,求直线l的方程;