题目内容
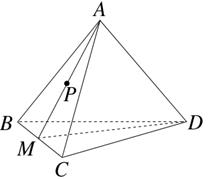
如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形,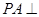 平面
平面 ,
, ,
, ,
, 依次是
依次是 的中点.
的中点.

(1)求证: ;
;
(2)求直线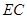 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,底面
中,底面 是矩形,
是矩形,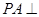 平面
平面 ,
, ,
, ,
, 依次是
依次是 的中点.
的中点.
(1)求证:
 ;
;(2)求直线
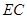 与平面
与平面 所成角的正弦值.
所成角的正弦值.(1)∵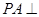 平面
平面 ,底面
,底面 是矩形,
是矩形,
∴ 平面
平面 ,∴
,∴ .∵
.∵ 是
是 的中点,
的中点,  ∴
∴ ,∵
,∵ ,∴
,∴ ;(2)直线
;(2)直线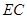 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .
.
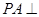 平面
平面 ,底面
,底面 是矩形,
是矩形,∴
 平面
平面 ,∴
,∴ .∵
.∵ 是
是 的中点,
的中点,  ∴
∴ ,∵
,∵ ,∴
,∴ ;(2)直线
;(2)直线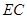 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .
.试题分析:(1)要证明直线
 ,即证明直线
,即证明直线 与平面
与平面 的两条相交的直线垂直,即证明
的两条相交的直线垂直,即证明 和
和 即可;(2)由题意知
即可;(2)由题意知 平面
平面 ,取
,取 中点
中点 ,
, 中点
中点 ,联结
,联结 ,则确定直线
,则确定直线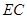 与平面
与平面 所成的角即为
所成的角即为 ,在
,在 中,易求出直线
中,易求出直线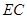 与平面
与平面 所成角的正弦值.
所成角的正弦值.试题解析:(1)∵
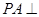 平面
平面 ,底面
,底面 是矩形
是矩形∴
 平面
平面 ∴
∴
∵
 是
是 的中点
的中点  ∴
∴
∵
 ∴
∴

(2)∵
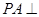 平面
平面 ,∴
,∴ ,
,又
 ,∴
,∴ 平面
平面 ,
, 取
 中点
中点 ,
, 中点
中点 ,联结
,联结 ,
,则
 且
且 ,
,∴
 是平行四边形,∴
是平行四边形,∴
∴
 即为直线
即为直线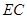 与平面
与平面 所成的角.
所成的角. 在
 中,
中, ,
,  ,
, ∴直线
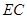 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .
. 
练习册系列答案
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
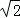 ,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2
,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2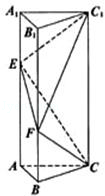



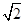 .
.