题目内容
已知函数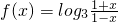 .
.
(1)判断并证明f(x)的奇偶性;
(2)当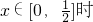 ,函数y=[f(x)]2-a•f(x)+1的最小值为
,函数y=[f(x)]2-a•f(x)+1的最小值为 ,求实数a的值.
,求实数a的值.
(1)证明:∵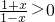 ,∴x∈(-1,1)
,∴x∈(-1,1)
函数的定义域为(-1,1)关于原点对称,…(2分)
又∵f(-x)+f(x)= =log31=0
=log31=0
∴f(-x(=-f(x)
故函数f(x)为奇函数(6分)
(2)解:令f(x)=t,∵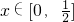 ,∴t∈[0,1]…(9分)
,∴t∈[0,1]…(9分)
函数
设函数y=[f(x)]2-a•f(x)+1的最小值为g(a)
若a≤0,则当t=0时,函数取到最小值g(a)=1;
由 =1,得a=-2
=1,得a=-2
若0<a<2,当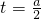 时,函数取到最小值
时,函数取到最小值
由 ,得
,得 (舍)
(舍)
若a≥2,当t=1时,函数取到最小值g(a)=2-a
由 ,解得a=4
,解得a=4
∴a=-2或a=4….(16分)
分析:(1)由题意可得函数的定义域为(-1,1)关于原点对称,然后检验f(-x)与f(x)的关系,即可判断
(2)令f(x)=t,由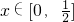 ,可得t∈[0,1],则函数
,可得t∈[0,1],则函数 ,,则通过讨论对称轴
,,则通过讨论对称轴 与区间[0,1]的关系可求
与区间[0,1]的关系可求
最小值为g(a),结合已知可求a
点评:本题主要考查对数函数的定义域与奇偶性,对a分类讨论是难点,由f(-x)+f(x)=0判断该题的奇偶性是好方法,属于中档题.
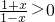 ,∴x∈(-1,1)
,∴x∈(-1,1)函数的定义域为(-1,1)关于原点对称,…(2分)
又∵f(-x)+f(x)=
 =log31=0
=log31=0∴f(-x(=-f(x)
故函数f(x)为奇函数(6分)
(2)解:令f(x)=t,∵
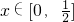 ,∴t∈[0,1]…(9分)
,∴t∈[0,1]…(9分)函数

设函数y=[f(x)]2-a•f(x)+1的最小值为g(a)
若a≤0,则当t=0时,函数取到最小值g(a)=1;
由
 =1,得a=-2
=1,得a=-2若0<a<2,当
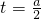 时,函数取到最小值
时,函数取到最小值
由
 ,得
,得 (舍)
(舍)若a≥2,当t=1时,函数取到最小值g(a)=2-a
由
 ,解得a=4
,解得a=4∴a=-2或a=4….(16分)
分析:(1)由题意可得函数的定义域为(-1,1)关于原点对称,然后检验f(-x)与f(x)的关系,即可判断
(2)令f(x)=t,由
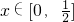 ,可得t∈[0,1],则函数
,可得t∈[0,1],则函数 ,,则通过讨论对称轴
,,则通过讨论对称轴 与区间[0,1]的关系可求
与区间[0,1]的关系可求最小值为g(a),结合已知可求a
点评:本题主要考查对数函数的定义域与奇偶性,对a分类讨论是难点,由f(-x)+f(x)=0判断该题的奇偶性是好方法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 ,
, 上的单调性;
上的单调性; .
. ,求a,b的值.
,求a,b的值. .
. 的奇偶性;(4分)
的奇偶性;(4分) 的方程
的方程 有两解,求实数
有两解,求实数 的取值范围;(6分)
的取值范围;(6分) ,记
,记 ,试求函数
,试求函数 在区间
在区间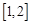 上的最大值.(10分)
上的最大值.(10分) .
. ,
, 的奇偶性;(2)求证:方程
的奇偶性;(2)求证:方程 至少有一根在区间
至少有一根在区间