题目内容
13.为了解适龄公务员对开放生育二胎政策的态度,某部门随机调查了90位三十岁到四十岁的公务员,得到如下列联表,因不慎丢失部分数据.(1))完成表格数据,判断是否有99%以上的把握认为“生二胎意愿与性别有关”并说明理由;
(2)已知15位有意愿生二胎的女性公务员中有两位来自省妇联,该部门打算从这15位有意愿生二胎的女性公务员中随机邀请两位来参加座谈,设邀请的2人中来自省妇联的人数为X,求X的分布列及数学期望E(X).
| 男性公务员 | 女性公务员 | 总计 | |
| 有意愿生二胎 | 15 | 45 | |
| 无意愿生二胎 | 25 | ||
| 总计 |
| P(k2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
分析 (1)由已知可得表格,利用K2计算公式即可得出.
(2))由题意可得,一名男公务员要生二胎意愿的概率为$\frac{30}{30+20}$=$\frac{3}{5}$,无意愿的概率为$\frac{20}{30+20}$$\frac{2}{5}$,记事件A:这三人中至少有一人要生二胎,且各人意愿相互独立.利用P(A)=1-P$(\overline{A})$即可得出.
(3)X可能的取值为0,1,2.利用P(X=k)=$\frac{{∁}_{13}^{2-k}{∁}_{2}^{k}}{{∁}_{15}^{2}}$,即可得出.
解答 解:(1)
| 男性公务员 | 女性公务员 | 总计 | |
| 有意愿生二胎 | 30 | 15 | 45 |
| 无意愿生二胎 | 20 | 25 | 45 |
| 总计 | 50 | 40 | 90 |
故没有99%以上的把握认为“生二胎意愿与性别有关”…(4分)
(2)由题意可得,一名男公务员要生二胎意愿的概率为$\frac{30}{30+20}$=$\frac{3}{5}$,无意愿的概率为$\frac{20}{30+20}$$\frac{2}{5}$,记事件A:这三人中至少有一人要生二胎,且各人意愿相互独立.
则P(A)=1-P$(\overline{A})$=1-$\frac{2}{5}×\frac{2}{5}×\frac{2}{5}$=$\frac{117}{125}$.
答:这三人中至少有一人有意愿生二胎的概率为$\frac{117}{125}$.…(8分)
(3)X可能的取值为0,1,2.利用P(X=k)=$\frac{{∁}_{13}^{2-k}{∁}_{2}^{k}}{{∁}_{15}^{2}}$,可得P(X=0)=$\frac{26}{35}$,P(X=1)=$\frac{26}{105}$,得P(X=2)=$\frac{1}{105}$.
| X | 0 | 1 | 2 |
| P | $\frac{26}{35}$ | $\frac{26}{105}$ | $\frac{1}{105}$ |
点评 本题考查了“独立性检验原理”、相互对立事件的概率计算公式、超几何分布列的性质及其数学期望计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.已知圆C1:x2+y2+4x-4y-3=0,动点P在圆C2:x2+y2-4x-12=0上,则△PC1C2面积的最大值为( )
| A. | 2$\sqrt{5}$ | B. | 4$\sqrt{5}$ | C. | 8$\sqrt{5}$ | D. | 20 |
4.已知双曲线x2-y2=1,点F1,F2为其两个焦点,点P为双曲线上一点,若|PF1|=1,则|PF2|=( )
| A. | 3 | B. | $2\sqrt{2}$ | C. | 4 | D. | 2 |
8.函数$y=sin2x-\sqrt{3}cos2x$的图象可由函数$y=sin2x+\sqrt{3}cos2x$的图象至少向右平移( )个单位长度得到.
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{π}{6}$ |
3.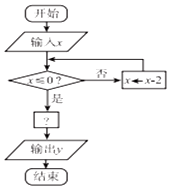 如图是一个算法的程序框图,当输入的x的值为7时,输出的 y值恰好是-1,则“?”处应填的关系式可能是( )
如图是一个算法的程序框图,当输入的x的值为7时,输出的 y值恰好是-1,则“?”处应填的关系式可能是( )
 如图是一个算法的程序框图,当输入的x的值为7时,输出的 y值恰好是-1,则“?”处应填的关系式可能是( )
如图是一个算法的程序框图,当输入的x的值为7时,输出的 y值恰好是-1,则“?”处应填的关系式可能是( )| A. | y=2x+1 | B. | y=3-x | C. | y=|x| | D. | y=log${\;}_{\frac{1}{3}}$x |
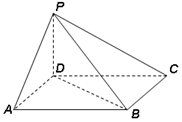 如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD=2,PD⊥面ABCD.
如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD=2,PD⊥面ABCD.