题目内容
已知函数f(x)=x3-ax-1,
(1)若函数f(x)在R上单调递增,求实数a的取值范围.
(2)若函数f(x)在区间(-1,1)上单调递减,求实数a的取值范围.
解: (1) ∵f′(x)=3x2-a, 由条件f′(x)≥0,即a≤3x2在x∈R时恒成立.
而3x2≥0, ∴a≤0, ∴实数a的取值范围是(-∞,0].
(2) 由条件f′(x)≤0 即a≥3x2在x∈(-1,1)时恒成立.
∵x∈(-1,1)时,3x2∈[0,3), ∴只要a≥3即可,
∴实数a的取值范围是[3,+∞).

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 的导数
的导数 处取到极大值,则
处取到极大值,则 的取值范围是 .
的取值范围是 . .
. 在区间
在区间 上是单调递增函数,则实数
上是单调递增函数,则实数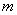 的取值范围是 .
的取值范围是 .  是减函数的区间为 ( D )
是减函数的区间为 ( D ) B.
B. C.
C. D.(0,2)
D.(0,2)  在
在 处取得极值.
处取得极值. 和
和 是函数
是函数 的极大值还是极小值;
的极大值还是极小值; 作曲线
作曲线 的切线,求此切线方程.
的切线,求此切线方程. 是复数,命题①若
是复数,命题①若 ,则
,则
 则
则 ③若
③若 ,则
,则
 ,以上真命题序号
,以上真命题序号  的焦点
的焦点 与双曲线
与双曲线 的右焦点重合,抛物线的准线与
的右焦点重合,抛物线的准线与 轴的交点为
轴的交点为 ,点
,点 在抛物线上且
在抛物线上且 ,则△
,则△ 的面积为
的面积为