题目内容
考察底为等腰直角三角形的直三棱柱的9条棱，甲从这9条棱中任选一条，乙从这9条棱中任选一条，则这两条棱互相垂直的概率为 （ ）
A．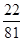
B．
C．
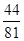D．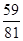
【答案】
C
【解析】略
练习册系列答案
相关题目
已知抛物线C：y2=
x，F为抛物线C的焦点，O为坐标原点，则在抛物线C上且满足△OFP为等腰直角三角形的点P的个数为（ ）
| 3 |
| 2 |
| A、2 | B、4 |
| C、2或4 | D、P点不存在 |
考察底为等腰直角三角形的直三棱柱的9条棱，甲从这9条棱中任选一条，乙从这9条棱中任选一条，则这两条棱互相垂直的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
