题目内容
已知两直线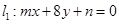 和直线
和直线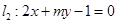 ,试确定
,试确定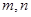 的值,使
的值,使
(1)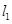 和
和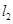 相交于点
相交于点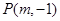 ;
;
(2)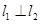 且
且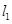 在y轴上的截距为
在y轴上的截距为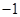 .
.
(1) ;(2)
;(2) .
.
解析试题分析:解题思路:(1)将 代入两直线方程,解关于
代入两直线方程,解关于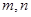 的方程组;(2)利用两个条件(垂直,则斜率之积为
的方程组;(2)利用两个条件(垂直,则斜率之积为 ;在
;在 轴上的截距为
轴上的截距为 ,化成斜截式),解关于
,化成斜截式),解关于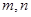 的方程组.
的方程组.
规律总结:涉及两直线的交点问题,即解方程组问题;涉及两直线的垂直、平行的判定,一般将直线化成斜截式方程再进行判定.注意点:一般式方程化成斜截式方程时,要注意直线的斜率是否存在(即 的系数是否为0).
的系数是否为0).
试题解析:(1)由题意: ,解得:
,解得: .
.
(2)由题意: ,所以:
,所以:
此时直线 的方程为:
的方程为: ,即
,即 ,令
,令 ,得
,得 .
.
考点:1两直线的交点;2.两直线垂直的判定.

练习册系列答案
相关题目
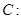
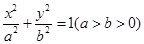 上的点到椭圆右焦点
上的点到椭圆右焦点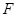 的最大距离为
的最大距离为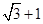 ,离心率
,离心率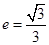 ,直线
,直线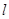 过点
过点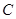 交于
交于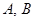 两点.
两点.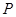 ,使得当
,使得当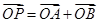 成立?若存在,求出所有点
成立?若存在,求出所有点 且垂直于直线
且垂直于直线 的直线方程的一般式方程为_____________
的直线方程的一般式方程为_____________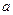 = 时,直线
= 时,直线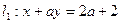 ,直线
,直线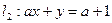 平行.
平行.