题目内容

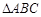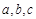已知在锐角中，为角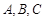所对的边，且.
(1)求角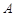的值；
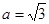(2)若，则求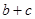的取值范围.

（1）；（2）.

解析试题分析：（1）先根据正弦定理将等式中的边换成角，进而根据余弦的二倍角公式、两角和与差公式进行化简得到，进而得到，结合角的范围即可得到的值；（2）根据正弦定理，将边转化成角即，进而根据三角形的内角和将其中的一个角换掉得到，然后根据题中条件确定的取值范围：，然后得到，进而根据三角函数的性质得到的取值范围.
（1）根据正弦定理，可将转化为，又由余弦的二倍角公式转化为
            2分
        4分
，因为在锐角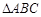中，所以                5分
（2）由（1）与正弦定理可得
所以                          6分
           8分
因为
所以                    10分.
考点：1.正弦定理；2.两角和差公式；3.二倍角公式；4.三角函数的图像与性质.

练习册系列答案
相关题目

在△ABC中，角A、B、C的对边分别为a、b、c，已知向量，，．
(1)求角C的大小；
(2)若，求角A的值．

在△ABC中，内角A，B，C的对边分别为a，b，c．已知＝．
(1)求的值；
(2)若B为钝角，b＝10，求a的取值范围．

在△ABC中，a，b，c分别是三内角A，B，C所对的三边，已知b2＋c2＝a2＋bc．
(1)求角A的大小；
(2)若2sin2＋2sin2＝1，试判断△ABC的形状．

已知锐角△ABC中，分别为角A、B、C所对的边，且.
(1) 求角C的大小；（2）若,且，求的值.

如图，公园有一块边长为2的等边△ABC的边角地，现修成草坪， 图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上．
(1)．设AD=x（x≥0），DE=y，求用x表示y的函数关系式,并求函数的定义域；
(2)．如果DE是灌溉水管，为节约成本，希望它最短，DE的位置应在哪里？如果DE是参观线路，则希望它最长，DE的位置又应在哪里？请予证明．

在中，角，，的对边分别为，，，若.
（1）求证：；
（2）当，时，求的面积.

在中，角A,B,C的对边分别为a,b,c，若.
（1）求B；
（2）设函数，求函数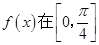上的取值范围.

在中，分别是角所对的边，且满足．
(1) 求的大小；
(2) 设向量，求的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网