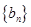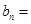题目内容
数列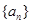 满足
满足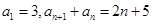 .
.
(1)求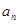 的表达式;
的表达式;
(2)令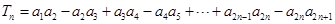 ,求
,求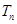 .
.
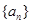 满足
满足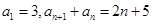 .
.(1)求
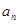 的表达式;
的表达式;(2)令
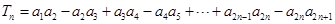 ,求
,求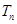 .
.(1)  ;(2)
;(2) 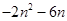
 ;(2)
;(2) 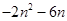
试题分析:(1)由于
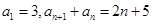 ,需要求数列的通项,本题是通过递推一项,然后将两式对减,即可得项数为奇和偶的通项公式,再归纳为一个通项公式即可.本小题常用构造的方法,构造一个新的等比数列,也可求得结论.
,需要求数列的通项,本题是通过递推一项,然后将两式对减,即可得项数为奇和偶的通项公式,再归纳为一个通项公式即可.本小题常用构造的方法,构造一个新的等比数列,也可求得结论.(2)由(1)得到通项公式,由题意可知前后两有一个公共项,所以通过提取公共项后另两项的差为定值,再运用通项公式即可得结论.本小题也可以通过先研究
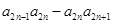 ,从而得到一个等差数列,即可得到结论.
,从而得到一个等差数列,即可得到结论.试题解析:(1)由
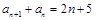 得:
得: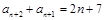 ,两式作差得:
,两式作差得: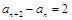 ,
,于是
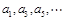 是首项
是首项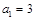 ,公差为
,公差为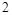 的等差数列,那么
的等差数列,那么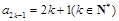 ,
,且
 是首项
是首项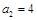 ,公差为
,公差为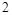 的等差数列,那么
的等差数列,那么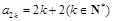 ,
,综上可知:
 .
.(2)
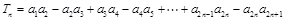
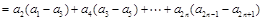
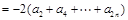
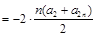
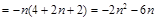 .
.
练习册系列答案
相关题目
 满足
满足 (
( ).
).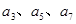 的值;
的值; (用含
(用含 的式子表示);
的式子表示); ,数列
,数列
 的前
的前 ,求
,求 的前
的前 项和
项和 满足
满足 ,等差数列
,等差数列 满足
满足 .
. ,求数列
,求数列 的前
的前 .
. 中,
中, ,对任意的
,对任意的 ,
, 成等比数列,公比为
成等比数列,公比为 ;
; 成等差数列,公差为
成等差数列,公差为 ,且
,且 .
. 的值;
的值;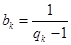 ,证明:数列
,证明:数列 为等差数列;
为等差数列; 的前
的前 项和
项和 .
. 中,已知
中,已知 .
. 分别为等差数列
分别为等差数列 的第3项和第5项,试求数列
的第3项和第5项,试求数列 项和
项和 。
。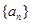 ,把
,把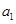 作为新数列
作为新数列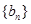 的第一项,把
的第一项,把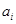 或
或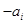 (
(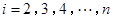 )作为新数列
)作为新数列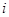 项,数列
项,数列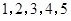 的一个生成数列是
的一个生成数列是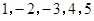 .已知数列
.已知数列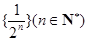 的生成数列,
的生成数列,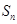 为数列
为数列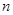 项和.
项和.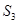 的所有可能值;
的所有可能值;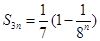 ,求数列
,求数列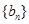 的通项公式;
的通项公式;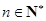 ,
,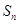 的所有可能值组成的集合为
的所有可能值组成的集合为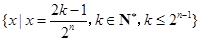 .
.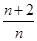 Sn(n=1,2,3,…),证明:
Sn(n=1,2,3,…),证明: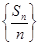 是等比数列;
是等比数列;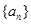 的前
的前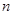 项和为
项和为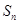 ,已知
,已知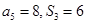 ,则
,则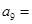 ( )
( ) B.
B. C.
C.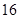 D 20
D 20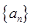 是等差数列,
是等差数列,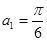 ,
,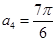 ,设
,设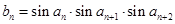 ,则数列
,则数列