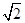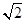题目内容
根据下列条件,求双曲线方程.
(1)与双曲线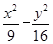 =1有共同的渐近线,且过点(-3,2
=1有共同的渐近线,且过点(-3,2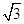 );
);
(2)与双曲线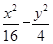 =1有公共焦点,且过点(3
=1有公共焦点,且过点(3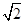 ,2).
,2).
(1)与双曲线
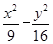 =1有共同的渐近线,且过点(-3,2
=1有共同的渐近线,且过点(-3,2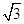 );
);(2)与双曲线
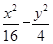 =1有公共焦点,且过点(3
=1有公共焦点,且过点(3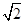 ,2).
,2).(1)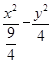 =1.(2)
=1.(2)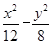 =1
=1
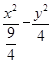 =1.(2)
=1.(2)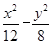 =1
=1解法1:(1)设双曲线的方程为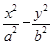 =1,
=1,
由题意,得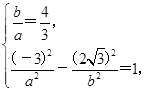
解得a2=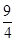 ,b2=4.所以双曲线的方程为
,b2=4.所以双曲线的方程为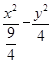 =1.
=1.
(2)设双曲线方程为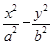 =1.由题意易求得c=2
=1.由题意易求得c=2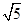 .
.
又双曲线过点(3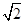 ,2),∴
,2),∴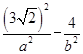 =1.又∵a2+b2=(2
=1.又∵a2+b2=(2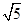 )2,∴a2=12,b2=8.
)2,∴a2=12,b2=8.
故所求双曲线的方程为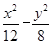 =1.
=1.
解法2:(1)设所求双曲线方程为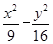 =λ(λ≠0),
=λ(λ≠0),
将点(-3,2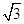 )代入得λ=
)代入得λ=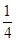 ,所以双曲线方程为
,所以双曲线方程为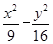 =
=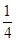 .
.
(2)设双曲线方程为 =1,
=1,
将点(3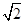 ,2)代入得k=4,所以双曲线方程为
,2)代入得k=4,所以双曲线方程为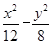 =1.
=1.
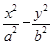 =1,
=1,由题意,得
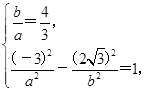
解得a2=
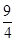 ,b2=4.所以双曲线的方程为
,b2=4.所以双曲线的方程为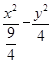 =1.
=1.(2)设双曲线方程为
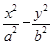 =1.由题意易求得c=2
=1.由题意易求得c=2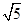 .
.又双曲线过点(3
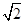 ,2),∴
,2),∴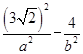 =1.又∵a2+b2=(2
=1.又∵a2+b2=(2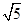 )2,∴a2=12,b2=8.
)2,∴a2=12,b2=8.故所求双曲线的方程为
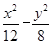 =1.
=1.解法2:(1)设所求双曲线方程为
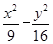 =λ(λ≠0),
=λ(λ≠0),将点(-3,2
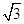 )代入得λ=
)代入得λ=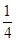 ,所以双曲线方程为
,所以双曲线方程为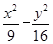 =
=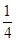 .
.(2)设双曲线方程为
 =1,
=1,将点(3
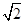 ,2)代入得k=4,所以双曲线方程为
,2)代入得k=4,所以双曲线方程为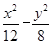 =1.
=1.
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
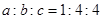 ,则双曲线
,则双曲线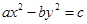 的离心率为( )
的离心率为( )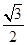
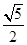
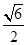
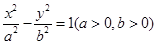 上任意一点P,作与实轴平行的直线,交两渐近线M,N两点,若
上任意一点P,作与实轴平行的直线,交两渐近线M,N两点,若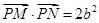 ,则该双曲线的离心率为____.
,则该双曲线的离心率为____.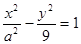 上一点,该双曲线的一条渐近线方程是
上一点,该双曲线的一条渐近线方程是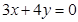 ,
,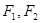 分别是双曲线的左、右焦点,若
分别是双曲线的左、右焦点,若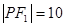 ,则
,则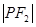 等于( )
等于( )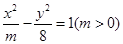 的一个焦点,则双曲线的离心率为( )
的一个焦点,则双曲线的离心率为( )