题目内容
已知命题p: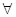 x1,x2
x1,x2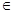 R,(f(x2)
R,(f(x2) f(x1))(x2
f(x1))(x2 x1)≥0,则
x1)≥0,则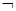 p是
p是
A.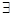 x1,x2 x1,x2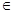 R,(f(x2) R,(f(x2) f(x1))(x2 f(x1))(x2 x1)≤0 x1)≤0 |
B.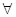 x1,x2 x1,x2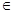 R,(f(x2) R,(f(x2) f(x1))(x2 f(x1))(x2 x1)≤0 x1)≤0 |
C.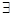 x1,x2 x1,x2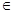 R,(f(x2) R,(f(x2) f(x1))(x2 f(x1))(x2 x1)<0 x1)<0 |
D.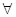 x1,x2 x1,x2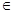 R,(f(x2) R,(f(x2) f(x1))(x2 f(x1))(x2 x1)<0 x1)<0 |
C
解析试题分析:全称命题的的否定是存在性命题。因为,命题p: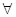 x1,x2
x1,x2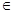 R,(f(x2)
R,(f(x2) f(x1))(x2
f(x1))(x2 x1)≥0,所以,
x1)≥0,所以,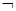 p是
p是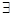 x1,x2
x1,x2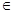 R,(f(x2)
R,(f(x2) f(x1))(x2
f(x1))(x2 x1)<0,选C。
x1)<0,选C。
考点:全称命题与存在性命题。
点评:简单题,全称命题的的否定是存在性命题。

练习册系列答案
相关题目
若 ,则“
,则“ ”是“
”是“ ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
条件 ,条件
,条件 ,则
,则 是
是 的
的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
已知a,b是实数,则“| a+b |=| a |+| b |”是“ab>0”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
设{an}(n∈N*)是等差数列,Sn是其前n项的和,且S5<S6,S6=S7>S8,则下列结论错误的是( )
| A.d<0 | B.a7=0 |
| C.S9>S5 | D.S6与S7均为Sn的最大值 |
“三角形有一个内角为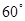 ”是“三内角成等差数列”的( )
”是“三内角成等差数列”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列命题中正确的是( )
| A.第一象限角必是锐角 | B.终边相同的角相等 |
| C.负角必是第四象限角 | D.相等的角终边必相同 |
函数f(x)=  在
在 上是单调函数的必要不充分条件是
上是单调函数的必要不充分条件是
A. | B. |
C. | D. |
 “是函数
“是函数 在区间
在区间 内单调递增”的( )
内单调递增”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |