题目内容
在平面直角坐标系xoy中,已知四点A(2,0),B(-2,0),C(0,-2),D(-2,-2),把坐标系平面沿y轴折为直二面角.
(1)求证:BC⊥AD;
(2)求三棱锥C-AOD的体积.

 解:(1)【法一】∵BOCD为正方形,
解:(1)【法一】∵BOCD为正方形,∴BC⊥OD,∠AOB为二面角B-CO-A的平面角
∴AO⊥BO,∵AO⊥CO,且BO∩CO=O
∴AO⊥平面BCO,又BC⊆平面BCO
∴AO⊥BC,且DO∩AO=O
∴BC⊥平面ADO,且AD⊆平面ADO,∴BC⊥AD.
【法二】分别以OA,OC,OB为x轴,y轴,z轴的正方向,建立空间直角坐标系,则
设O(0,0,0),A(2,0,0),B(0,0,2),C(0,2,0),D(0,2,2);
有
 =(-2,2,2),
=(-2,2,2), =(-2,2,0),∴
=(-2,2,0),∴ •
• =0,∴
=0,∴ ⊥
⊥ ,即BC⊥AD.
,即BC⊥AD.(2)三棱锥C-AOD的体积为:VC-AOD=VA-COD=
 •S△COD•OA
•S△COD•OA=
 ×
× ×2×2×2=
×2×2×2= .
.分析:(1)【法一】要证异面直线BC⊥AD,须证BC⊥平面ADO,即证AO⊥BC,BC⊥OD,这是成立的;
【法二】建立空间直角坐标系,
由向量的数量积为0,得两向量垂直.
(2)三棱锥的体积由体积公式V=
 •S高•h可得.
•S高•h可得.点评:本题考查了空间中的垂直关系,可以直接证明线线垂直,得线面垂直;线面垂直,得线线垂直.用向量的数量积为0,证线线垂直更容易.求三棱锥的体积是关键是求底面积和高.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
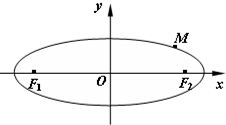 如图,在平面直角坐标系xoy中,已知椭圆C:
如图,在平面直角坐标系xoy中,已知椭圆C: