题目内容
已知α、β都是锐角, 的值为( )
的值为( )A.

B.

C.

D.

【答案】分析:由已知中α、β都是锐角,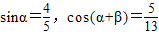 ,我们根据同角三角函数关系公式,可以求出cosα,sin(α+β),代入两角差的正弦函数公式,即可求出答案.
,我们根据同角三角函数关系公式,可以求出cosα,sin(α+β),代入两角差的正弦函数公式,即可求出答案.
解答:解:∵α、β都是锐角,
又∵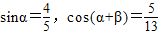 ,
,
∴cosα= ,sin(α+β)=
,sin(α+β)=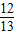
∴sinβ=sin[(α+β)-α]=sin(α+β)•cosα-cos(α+β)•sinα=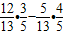 =
=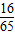
故选C
点评:本题考查的知识点是同角三角函数的基本关系公式,两角差的正弦函数公式,其中根据已知条件求出cosα,sin(α+β),为两角差的正弦函数公式的使用准备好所有的数据是解答本题的关键.
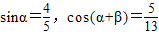 ,我们根据同角三角函数关系公式,可以求出cosα,sin(α+β),代入两角差的正弦函数公式,即可求出答案.
,我们根据同角三角函数关系公式,可以求出cosα,sin(α+β),代入两角差的正弦函数公式,即可求出答案.解答:解:∵α、β都是锐角,
又∵
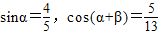 ,
,∴cosα=
 ,sin(α+β)=
,sin(α+β)=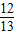
∴sinβ=sin[(α+β)-α]=sin(α+β)•cosα-cos(α+β)•sinα=
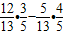 =
=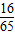
故选C
点评:本题考查的知识点是同角三角函数的基本关系公式,两角差的正弦函数公式,其中根据已知条件求出cosα,sin(α+β),为两角差的正弦函数公式的使用准备好所有的数据是解答本题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 ,(1+tanA)(1+tanB)=2,求证A+B=45°.
,(1+tanA)(1+tanB)=2,求证A+B=45°.