题目内容
如图,A为双曲线M:x2-y2=1的右顶点,平面上的动点P到点A的距离与到直线l:x=-1的距离相等.(Ⅰ) 求动点P的轨迹N的方程;
(Ⅱ)已知双曲线M的两条渐近线分别与轨迹N交于点B,C(异于原点).试问双曲线M上是否存在一点D,满足
 ?若存在,求出点D坐标;若不存在,请说明理由.
?若存在,求出点D坐标;若不存在,请说明理由.
【答案】分析:(1)方法一:设点P(x,y),点P到直线l的距离为d,利用|PA|=d,建立方程,化简可得动点P的轨迹N的方程;
方法二:由抛物线定义知:动点P的轨迹N是以A(1,0)为焦点,直线l:x=-1为准线的抛物线,故可求动点P的轨迹N的方程;
(2)双曲线M的渐近线方程与抛物线方程联立,可得点B、C的坐标,设点D(x,y),则|x|≥1,利用 ,即可得到结论.
,即可得到结论.
解答:解:(1)方法一:依题意,A(1,0)
设点P(x,y),点P到直线l的距离为d,则|PA|=d
即
 ,化简得:y2=4x
,化简得:y2=4x
方法二:依题意,A(1,0)
由抛物线定义知:动点P的轨迹N是以A(1,0)为焦点,直线l:x=-1为准线的抛物线,其方程为y2=4x.
(2)双曲线M的渐近线方程为y=±x
联立抛物线方程y2=4x,可得点B(4,4)、C(4,-4)
设点D(x,y),则|x|≥1
若 ,则(x-4)2+y2-16=(x-1)2+y2
,则(x-4)2+y2-16=(x-1)2+y2
∴
∵|x|≥1,∴不存在点D满足题意.
点评:本题主要考查抛物线的定义、双曲线的性质、向量数量积等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想
方法二:由抛物线定义知:动点P的轨迹N是以A(1,0)为焦点,直线l:x=-1为准线的抛物线,故可求动点P的轨迹N的方程;
(2)双曲线M的渐近线方程与抛物线方程联立,可得点B、C的坐标,设点D(x,y),则|x|≥1,利用
 ,即可得到结论.
,即可得到结论.解答:解:(1)方法一:依题意,A(1,0)
设点P(x,y),点P到直线l的距离为d,则|PA|=d
即

 ,化简得:y2=4x
,化简得:y2=4x方法二:依题意,A(1,0)
由抛物线定义知:动点P的轨迹N是以A(1,0)为焦点,直线l:x=-1为准线的抛物线,其方程为y2=4x.
(2)双曲线M的渐近线方程为y=±x
联立抛物线方程y2=4x,可得点B(4,4)、C(4,-4)
设点D(x,y),则|x|≥1
若
 ,则(x-4)2+y2-16=(x-1)2+y2
,则(x-4)2+y2-16=(x-1)2+y2∴

∵|x|≥1,∴不存在点D满足题意.
点评:本题主要考查抛物线的定义、双曲线的性质、向量数量积等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想

练习册系列答案
相关题目
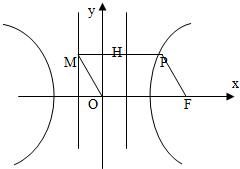 如图,F为双曲线C:
如图,F为双曲线C: 如图,F为双曲线
如图,F为双曲线 如图,A为双曲线M:x2-y2=1的右顶点,平面上的动点P到点A的距离与到直线l:x=-1的距离相等.
如图,A为双曲线M:x2-y2=1的右顶点,平面上的动点P到点A的距离与到直线l:x=-1的距离相等.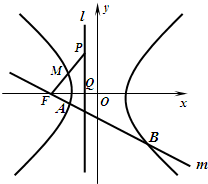 如图点F为双曲线C的左焦点,左准线l交x轴于点Q,点P是l上的一点|PQ|=|FQ|=1,且线段PF的中点M在双曲线C的左支上.
如图点F为双曲线C的左焦点,左准线l交x轴于点Q,点P是l上的一点|PQ|=|FQ|=1,且线段PF的中点M在双曲线C的左支上.