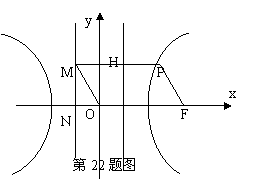
题目内容
 如图,F为双曲线C:
如图,F为双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
| PF |
| OF |
分析:作双曲线的右准线交PM于H,由平行四边形OFPM的性质和双曲线中的基本概念,算出|PH|=|OF|-|MH|=c-
,再根据圆锥曲线的统一定义列式,结合题意化简整理,即可得到离心率e与λ的关系式.
| 2a2 |
| c |
解答:解:∵四边形OFPM是平行四边形,∴|OF|=|PM|=c,
作双曲线的右准线,交PM于H,
则|PM|=|PH|+|MH|=|OF|,可得|PH|=|OF|-|MH|=c-
,
由圆锥曲线的统一定义,得
=e,
结合|
|=λ|
|,得
=e即
=e,
∴
=
=e,
去分母化简得e2-λe-2=0,即为所求离心率e与λ的关系式.
作双曲线的右准线,交PM于H,
则|PM|=|PH|+|MH|=|OF|,可得|PH|=|OF|-|MH|=c-
| 2a2 |
| c |
由圆锥曲线的统一定义,得
| |PF| |
| |PH| |
结合|
| PF |
| OF |
| λ|OF| | ||
c-
|
| λc | ||
c-
|
∴
| λ | ||
1-
|
| λ | ||
1-
|
去分母化简得e2-λe-2=0,即为所求离心率e与λ的关系式.
点评:本题给出双曲线满足的条件,求关于离心率e的关系式.着重考查了双曲线的定义与标准方程、圆锥曲线的统一定义等知识,属于中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
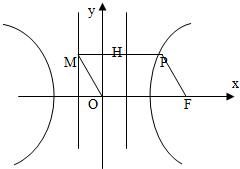 如图,F为双曲线C:
如图,F为双曲线C: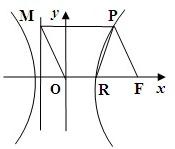 如图,F为双曲线C:
如图,F为双曲线C: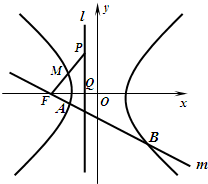 如图点F为双曲线C的左焦点,左准线l交x轴于点Q,点P是l上的一点|PQ|=|FQ|=1,且线段PF的中点M在双曲线C的左支上.
如图点F为双曲线C的左焦点,左准线l交x轴于点Q,点P是l上的一点|PQ|=|FQ|=1,且线段PF的中点M在双曲线C的左支上.