题目内容
13.(1)已知一条直线经过点$P({-2,\sqrt{3}})$,Q(-1,0),求直线PQ的方程.(用一般式表示)(2)已知一条直线经过点P(2,3),且在x轴,y轴上的截距相等,求该直线的方程.(用一般式表示)
分析 (1)求出直线PQ的斜率,从而求出直线方程即可;(2)通过讨论直线过(0,0)和直线不过(0,0)求出直线方程即可.
解答 解:(1)$P({-2,\sqrt{3}})$,Q(-1,0),
故KPQ=$\frac{\sqrt{3}}{-2-(-1)}$=-$\sqrt{3}$,
故直线PQ的方程是:y=-$\sqrt{3}$(x+1),
即$\sqrt{3}$x+y+$\sqrt{3}$=0;
(2)由直线在x轴,y轴上的截距相等,
则直线不过(0,0)时,
设直线方程是:x+y=a,
将P(2,3)代入方程得:a=5,
故直线方程是:x+y-5=0;
直线过(0,0)时,直线的斜率k=$\frac{3}{2}$,
故直线方程是:y=$\frac{3}{2}$x,即3x-2y=0.
点评 本题考查了求直线方程问题,考查直线的斜率和直线的点斜式方程以及一般式方程,是一道基础题.

练习册系列答案
相关题目
3.函数f(x)=9x-3x+1+2(-1≤x≤1)的值域为( )
| A. | $[{\frac{9}{19},2}]$ | B. | [-1,2] | C. | $[{-\frac{1}{4},2}]$ | D. | $[{-\frac{1}{4},+∞})$ |
1.若m=60,n=40,按照如图所示的程序框图运行后,输出的结果是( )


| A. | $\frac{1}{200}$ | B. | 200 | C. | 20 | D. | 2 |
8.斜率为k的直线y-4=-k(x+3)所过的定点是( )
| A. | (-3,4) | B. | (-3,-4) | C. | (3,4) | D. | (3,-4) |
18.已知两点A(6,5)为圆心,$\sqrt{10}$为半径的圆的标准方程为( )
| A. | (x-6)2+(y-5)2=10 | B. | (x+6)2+(y+5)2=10 | C. | (x-5)2+(y-6)2=$\sqrt{10}$ | D. | (x+5)2+(y+6)2=$\sqrt{10}$ |
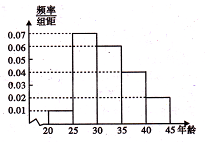 某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.把符合条件的1000名志愿者按年龄分组:第1组[20,25)、第2组[25,30)、第3组[30,35)、第4组[35,40)、第5组[40,45),得到的频率分布直方图如图所示:
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.把符合条件的1000名志愿者按年龄分组:第1组[20,25)、第2组[25,30)、第3组[30,35)、第4组[35,40)、第5组[40,45),得到的频率分布直方图如图所示: