题目内容
17．设x1，x2∈R，现定义运算“?”：x1?x2=（x1+x2）2-（x1-x2）2，若x≥0，则动点P（x，$\sqrt{x?2}$）的轨迹是（ ）| A． | 椭圆的一部分 | B． | 双曲线的一部分 | C． | 抛物线的一部分 | D． | 圆的一部分 |
分析 利用定义可得方程，即可求出动点P（x，$\sqrt{x?2}$）的轨迹．
解答 解：由题意，y=$\sqrt{x?2}$=$\sqrt{（x+2）^{2}-（x-2）^{2}}$（x≥0），
∴y2=8x（x≥0），
∴动点P（x，$\sqrt{x?2}$）的轨迹是抛物线的一部分．
故选：C．
点评 本题考查动点P（x，$\sqrt{x?2}$）的轨迹，考查新定义，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
7．已知正方体ABCD-A1B1C1D1的棱长为1，M为棱CC1的中点，则点M到平面A1BD的距离是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{2\sqrt{2}}}{3}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
8．已知a，b∈R，且ab≠0，那么“a＞b”是“lg（a-b）＞0”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
5．“?n∈N*，a${\;}_{n+1}^{2}$=anan+2”是“数列{an}为等比数列”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
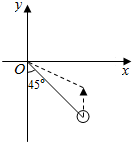如图，据气象部门预报，在距离码头O南偏东45°方向600km处的热带风暴中心正以20km/h的速度向正北方向移动，距台风中心450km以内的地区都将受到影响．据以上预报估计，从现在起多长时间后，该码头将受到热带风暴的影响，影响时间大约有多长？（精确到0.1h，$\sqrt{2}≈$1.414）
2．设函数f（x）是定义在R上的函数，则“x0是函数f（x）的极值点”是“f′（x0）=0”的（ ）条件．
| A． | 充分不必要 | B． | 必要不充分 | ||
| C． | 充要 | D． | 既不充分也不必要 |
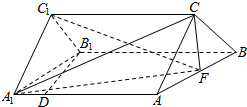已知三棱柱ABC-A1B1C1中，AA1⊥平面ABC，△ABC为边长为1的正三角形，且AA1=2，D为AA1上的点，且A1D=$\frac{1}{4}$，F为AB的中点．
7．函数f（x）=$\frac{{2}^{x}+1}{{2}^{x}-1}$是（ ）
| A． | 奇函数 | B． | 偶函数 | ||
| C． | 非奇非偶函数 | D． | 既是奇函数又是偶函数 |