题目内容
如图所示，矩形ABCD中，AD⊥平面ABE，AE＝EB＝BC＝2，F为CE上的点，且BF⊥平面ACE.
(1)求证：AE⊥平面BCE；
(2)求证：AE∥平面BFD；
(3)求三棱锥C－BGF的体积．
【答案】
(1)证明 ∵AD⊥平面ABE，AD∥BC， ∴BC⊥平面ABE，则AE⊥BC.
又∵BF⊥平面ACE，则AE⊥BF，
又BC∩BF＝B，∴AE⊥平面BCE.
(2)证明 由题意可得G是AC的中点，连结FG，
∵BF⊥平面ACE，∴CE⊥BF.
而BC＝BE，∴F是EC的中点，
在△AEC中，FG∥AE，∴AE∥平面BFD.
(3)∵AE∥FG.
而AE⊥平面BCE，
∴FG⊥平面BCF.
∵G是AC中点，F是CE中点，
∴FG∥AE且FG＝AE＝1.
∴Rt△BCE中，BF＝CE＝CF＝，
∴S△CFB＝××＝1.
∴VC－BGF＝VG－BCF＝·S△CFB·FG＝×1×1＝
【解析】略
练习册系列答案
相关题目
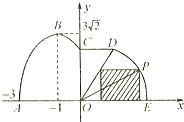如图，某市拟在道路的一侧修建一条运动赛道，赛道的前一部分为曲线段ABC，该曲线段为函数y=Asin（ωx+φ）（A＞0，ω＞0，
如图所示，在△ABC中，AC=1，AB=3，∠ACB=
如图所示，在△ABC中，AC=1，AB=3，∠ACB=
＜φ＜π），x∈[-3，0]的图象，且图象的最高点为B（-1，3
）；赛道的中间部分为
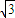千米的水平跑到CD；赛道的后一部分为以O圆心的一段圆弧
．
(A＞0，
＞0，
＜
＜
)，x∈[－3，0]的图象，且图象的最高点为B(－1，
)；赛道的中间部分为
千米的水平跑到CD；赛道的后一部分为以O圆心的一段圆弧
．
，求当“矩形草坪”的面积最大时