题目内容
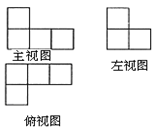
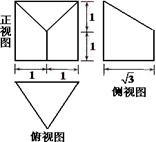
(本小题满分14分)如图,一简单几何体有五个顶点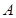 、
、 、
、 、
、 、
、 ,它的一个面
,它的一个面 内接于⊙
内接于⊙ ,
, 是⊙
是⊙ 的直径,四边形
的直径,四边形 为平行四边形,
为平行四边形, 平面
平面 .
.
(1)证明:平面
 平面
平面 ;
;
(2)若 ,
, ,
, ,求该简单几何体的体积.
,求该简单几何体的体积.
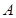 、
、 、
、 、
、 、
、 ,它的一个面
,它的一个面 内接于⊙
内接于⊙ ,
, 是⊙
是⊙ 的直径,四边形
的直径,四边形 为平行四边形,
为平行四边形, 平面
平面 .
.(1)证明:平面

 平面
平面 ;
;(2)若
 ,
, ,
, ,求该简单几何体的体积.
,求该简单几何体的体积.
(1)见解析;(2)1.
第一问要证明面面垂直,关键是证明线面垂直,借助于面面垂直的判定定理得到结论即可即证 平面
平面
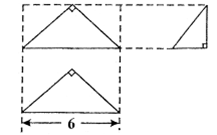
第二问中,将该几何体的体积分解为两个三棱锥的体积即可。注意合理分解为两个特殊几何体的体积是解决该试题的关键。
解: (1)证明: 平面
平面 ,
, 平面
平面 ,
,
 . ………1分
. ………1分
 是⊙
是⊙ 的直径,
的直径,
 , ………2分
, ………2分
又 ………3分
………3分
 平面
平面 , ………4分
, ………4分

 平面
平面 ………5分
………5分
又 平面
平面 ………6分
………6分
 平面
平面
 平面
平面 . ………7分
. ………7分
(2)设所求简单几何体的体积为 ,
,

 平面
平面
 平面
平面
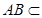 平面
平面


在 中
中


 ………8分
………8分
方法一: 连 ,由(1),(2)知
,由(1),(2)知 是三棱锥
是三棱锥 的高,
的高, 是三棱锥
是三棱锥 的高
的高
 ………9分
………9分
 ………11分
………11分
 ………13分
………13分
 该简单组合体的体积
该简单组合体的体积 . ………14分
. ………14分
方法二:
 平面
平面 ,
,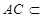 平面
平面 ,
,
 .
.
又由(1)知 ,
,
又
 平面
平面 ,
,
 是四棱锥
是四棱锥 的高,且由(1),(2)证明易知四边形
的高,且由(1),(2)证明易知四边形 为边长为
为边长为 的正方形. ………10分
的正方形. ………10分
 ………11分
………11分
 ………12分
………12分
 ………13分
………13分

 ………14分
………14分
 平面
平面
第二问中,将该几何体的体积分解为两个三棱锥的体积即可。注意合理分解为两个特殊几何体的体积是解决该试题的关键。
解: (1)证明:
 平面
平面 ,
, 平面
平面 ,
, . ………1分
. ………1分 是⊙
是⊙ 的直径,
的直径,
 , ………2分
, ………2分又
 ………3分
………3分 平面
平面 , ………4分
, ………4分
 平面
平面 ………5分
………5分又
 平面
平面 ………6分
………6分 平面
平面
 平面
平面 . ………7分
. ………7分(2)设所求简单几何体的体积为
 ,
,
 平面
平面
 平面
平面
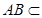 平面
平面


在
 中
中

 ………8分
………8分方法一: 连
 ,由(1),(2)知
,由(1),(2)知 是三棱锥
是三棱锥 的高,
的高, 是三棱锥
是三棱锥 的高
的高 ………9分
………9分 ………11分
………11分 ………13分
………13分 该简单组合体的体积
该简单组合体的体积 . ………14分
. ………14分方法二:
 平面
平面 ,
,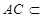 平面
平面 ,
, .
. 又由(1)知
 ,
, 又

 平面
平面 ,
,  是四棱锥
是四棱锥 的高,且由(1),(2)证明易知四边形
的高,且由(1),(2)证明易知四边形 为边长为
为边长为 的正方形. ………10分
的正方形. ………10分 ………11分
………11分 ………12分
………12分 ………13分
………13分
 ………14分
………14分
练习册系列答案
相关题目