题目内容
在数列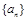 中,
中,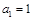 ,且对任意的
,且对任意的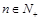 ,都有
,都有 .
.
(1)求证:数列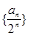 是等差数列;
是等差数列;
(2)设数列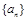 的前
的前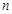 项和为
项和为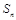 ,求证:对任意的
,求证:对任意的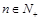 ,
,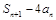 都为定值.
都为定值.
【答案】
证明: (1)∵ ,∴
,∴ .
.
∴数列 是以
是以 为首项,
为首项, 为公差的等差数列.
为公差的等差数列.
(2) 由(1)知 ,∴
,∴ .
.
∴ .…………………………①
.…………………………①
∴ .……………………………………②
.……………………………………②
∴由②-①可得 .
.
∴ ,故结论成立.
,故结论成立.
【解析】略

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
 中,
中,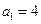 且对任意
且对任意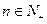 均有:
均有: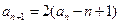
 是等比数列;
是等比数列;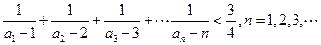
 中,如果对任意的
中,如果对任意的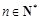 ,都有
,都有 (
( 为常数),则称数列
为常数),则称数列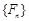 满足
满足 ,
, ,
,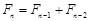 (
(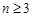 ),则该数列不是比等差数列;②若数列
),则该数列不是比等差数列;②若数列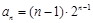 ,则数列
,则数列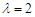 ;③等比数列一定是比等差数列,等差数列不一定是比等差数列;④若
;③等比数列一定是比等差数列,等差数列不一定是比等差数列;④若 是等比数列,则数列
是等比数列,则数列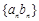 是比等差数列.
是比等差数列. 中,
中, 且对任意
且对任意 均有:
均有:
 是等比数列;
是等比数列;
 中,
中, 且对任意大于1的正整数
且对任意大于1的正整数 ,点
,点 在直线
在直线 上,则
上,则 .
.