题目内容
在数列 中,如果对任意的
中,如果对任意的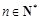 ,都有
,都有 (
( 为常数),则称数列
为常数),则称数列 为比等差数列,
为比等差数列, 称为比公差.现给出以下命题:①若数列
称为比公差.现给出以下命题:①若数列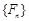 满足
满足 ,
, ,
,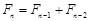 (
(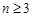 ),则该数列不是比等差数列;②若数列
),则该数列不是比等差数列;②若数列 满足
满足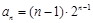 ,则数列
,则数列 是比等差数列,且比公差
是比等差数列,且比公差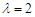 ;③等比数列一定是比等差数列,等差数列不一定是比等差数列;④若
;③等比数列一定是比等差数列,等差数列不一定是比等差数列;④若 是等差数列,
是等差数列, 是等比数列,则数列
是等比数列,则数列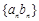 是比等差数列.
是比等差数列.
其中所有真命题的序号是_________________.
【答案】
①③
【解析】
试题分析:根据新定义可知:①若数列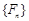 满足
满足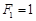 ,
,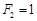 ,
,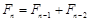 (
(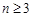 ),则该数列不是比等差数列:因为
),则该数列不是比等差数列:因为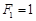 ,
,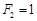 ,
,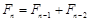 ,所以
,所以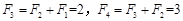 ,所以
,所以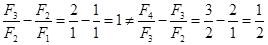 ,所以不成立。
,所以不成立。
②若数列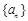 满足
满足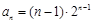 ,则数列
,则数列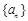 是比等差数列,且比公差
是比等差数列,且比公差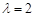 :因为
:因为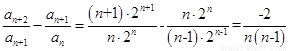 不是常数,所以不成立;
不是常数,所以不成立;
③等比数列一定是比等差数列,等差数列不一定是比等差数列:若数列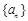 是等比数列,则
是等比数列,则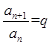 ,所以
,所以 ,所以是比等差数列,成立;
,所以是比等差数列,成立;
④若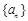 是等差数列,
是等差数列,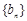 是等比数列,则数列
是等比数列,则数列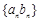 是比等差数列:当
是比等差数列:当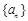 和
和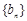 是非0常数列时,成立,其他的不一定成立。
是非0常数列时,成立,其他的不一定成立。
考点:数列的应用。
点评:本题考查新定义的理解和运算,解决该试题的关键是应正确理解新定义,并结合所学知识来判定,同时注意利用列举法判断命题为假

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
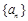 中,如果对任意的
中,如果对任意的 ,都有
,都有 (
( 为常数),则称数列
为常数),则称数列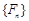 满足
满足 ,
,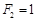 ,
,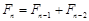 (
(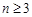 ),则该数列不是比等差数列;②若数列
),则该数列不是比等差数列;②若数列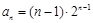 ,则数列
,则数列 ;③等比数列一定是比等差数列,等差数列不一定是比等差数列;④若
;③等比数列一定是比等差数列,等差数列不一定是比等差数列;④若 是等比数列,则数列
是等比数列,则数列 是比等差数列.
是比等差数列.