题目内容
(数列)若等比数列{an}满足a2a4=
,则a1a3a5=
| 1 |
| 2 |
±
| ||
| 4 |
±
.
| ||
| 4 |
分析:根据等比数列的性质:若m+n=p+q=2r,则aman=apaq=ar2即可求得a1a3a5的值.
解答:解:∵数列{an}是等比数列,∴a2a4=a1a5=a32=
,
∴a3=±
,
∴a1a3a5=(a1a5)a3=
×(±
)=±
.
故答案为±
.
| 1 |
| 2 |
∴a3=±
| ||
| 2 |
∴a1a3a5=(a1a5)a3=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
故答案为±
| ||
| 4 |
点评:本题考查了等比数列中的有关计算,熟记通项公式及求和公式是解题的基础,灵活运用性质可简化运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
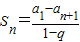 ;
; ,则a1a3a5= .
,则a1a3a5= .